Exploring Dilations
A dilation is a type of transformation. Other transformations include translations, reflections, and rotations.
The result of a transformation is called the image. The original figure is called the pre-image.
Use the link below to explore dilations:
- Click on the ACTIVITIES button at the top of the screen.
- Follow the directions for “Playing with Dilations” that appear on the right side of the screen.
- Click on either the left or right arrow near the top right of the screen. Follow the directions for “Hitting a Target” that appear on the right side of the screen.
After you have explored some dilations, answer the following questions in your math journal. Use the words pre-image and image in your responses.
- When you dragged the blue slider, how did the image compare to the pre-image? What stayed the same? What changed?
- When you rotated the pre-image, how did the image compare to the pre-image? What stayed the same? What changed?
- When you dragged the black point on the white line (the center of dilation), how did the image compare to the pre-image? What stayed the same? What changed?
- Use the word bank to complete the sentences below:
- A dilation is a transformation that changes the __________ and ____________ of a figure. A dilation does not change the figure’s _____________.
- The result of a dilation is called the ________. The original figure is called the __________.
- If the image is smaller than the pre-image, the dilation is a __________.
- If the image is larger than the pre-image, the dilation is a __________.
WORD BANK:
pre-image, size, enlargement, position, image, orientation, reduction

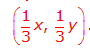 .
.