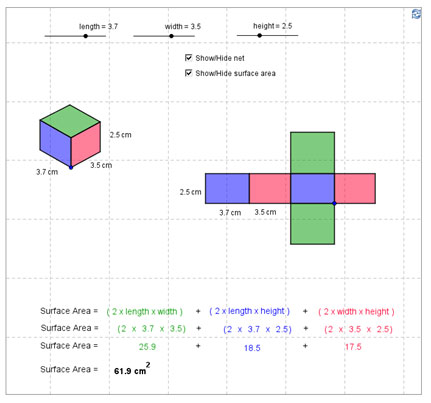
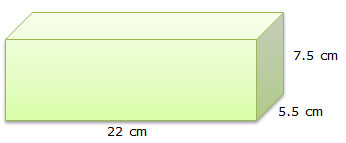
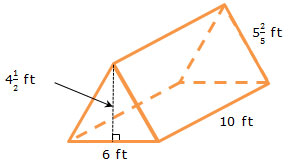
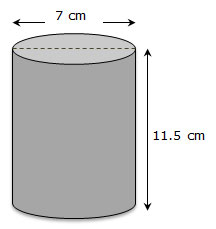
Recall that similar figures have the same shape but not necessarily the same size. You can also generate similar figures using a scale factor.
Consider the two rectangles shown below.

The angles in Rectangle 1 are congruent to the corresponding angles in Rectangle 2. After all, a rectangle contains four right angles, and all right angles are congruent. However, the sides are not congruent. Let's take a closer look at the side lengths using proportions.
Since the ratios of the corresponding side lengths are proportional, we can say that the rectangles are similar.
We can also use the ratios of corresponding sides to identify the scale factor that is used to generate Rectangle 2 from Rectangle 1.

In this example, the scale factor is because the dimensions of Rectangle 1 are multiplied by to generate the dimensions of Rectangle 2.
How does this dilation affect the area of the new rectangle? You will investigate that relationship.