You’ve used probability to describe the likelihood of events occurring. In this lesson, you will investigate how you can calculate the probability of two or more events.
Probability is used to describe how likely something is to happen. For example, you may have heard the weather forecaster describe the chances that it will rain today. She is using probability to make that forecast.
Probability is formally defined as the ratio of the number of desired outcomes (what you want to happen) to the number of total possible outcomes (what could possibly happen). Probability is a ratio, so it can be expressed as a fraction, a decimal, or a percent.


The probability of rain today is 80%. That means that there is an 80% chance that the event of rain will occur.

Out of a dozen dyed eggs, there are 2 blue ones. The probability of randomly choosing a blue egg is . Since this is only one event occurring, this is called a simple event.

There is a 7 out of 10 chance that someone will catch the flu if they don't get a flu shot. The probability of getting the flu is 0.7.

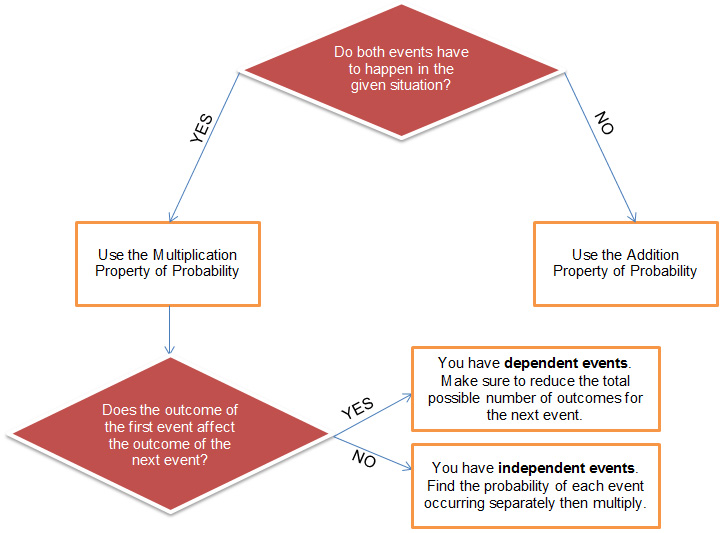
 The relationship between multiple events that occur is important. Sometimes, when an event occurs, it does not affect the chances of the next event(s) occurring. For example, when you roll a pair of number cubes, the number that lands on the top face of one number cube does not affect the number that lands on the top of the second number cube.
The relationship between multiple events that occur is important. Sometimes, when an event occurs, it does not affect the chances of the next event(s) occurring. For example, when you roll a pair of number cubes, the number that lands on the top face of one number cube does not affect the number that lands on the top of the second number cube.
 Hot Tip!
Hot Tip!
 Ms. Dawson’s 1st period science class has 18 girls and 12 boys. Ms. Dawson needs to select a pair of students to help her set up a laboratory investigation. She has decided to randomly select 2 students from the entire class.
Ms. Dawson’s 1st period science class has 18 girls and 12 boys. Ms. Dawson needs to select a pair of students to help her set up a laboratory investigation. She has decided to randomly select 2 students from the entire class.