Components of Vectors
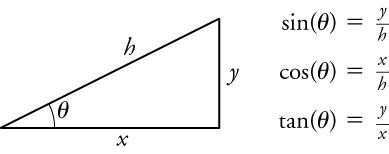
For the analytical method of vector addition and subtraction, we use some simple geometry and trigonometry, instead of using a ruler and protractor as we did for graphical methods. However, the graphical method will still come in handy to visualize the problem by drawing vectors using the head-to-tail method. The analytical method is more accurate than the graphical method, which is limited by the precision of the drawing. For a refresher on the definitions of the sine, cosine, and tangent of an angle, see Figure 5.18.
Since, by definition, , we can find the length x if we know h and by using . Similarly, we can find the length of y by using . These trigonometric relationships are useful for adding vectors.
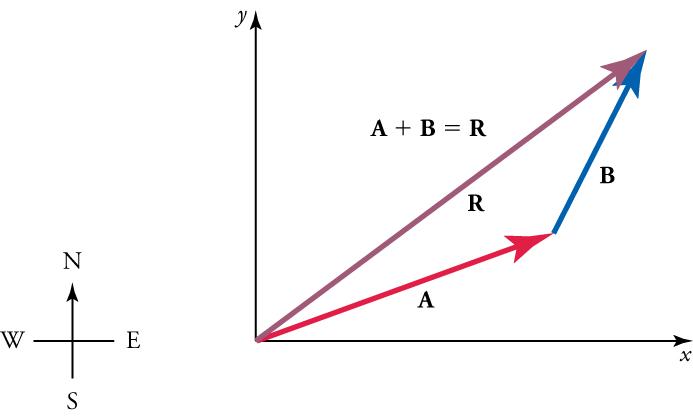
When a vector acts in more than one dimension, it is useful to break it down into its x and y components. For a two-dimensional vector, a component is a piece of a vector that points in either the x- or y-direction. Every 2-d vector can be expressed as a sum of its x and y components.
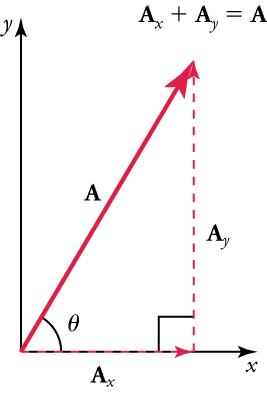
For example, given a vector likein Figure 5.19, we may want to find what two perpendicular vectors,and, add to produce it. In this example,andform a right triangle, meaning that the angle between them is 90 degrees. This is a common situation in physics and happens to be the least complicated situation trigonometrically.
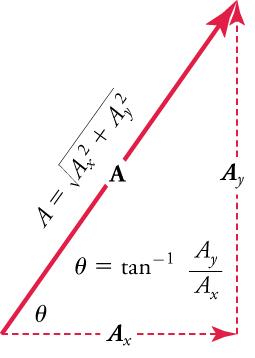
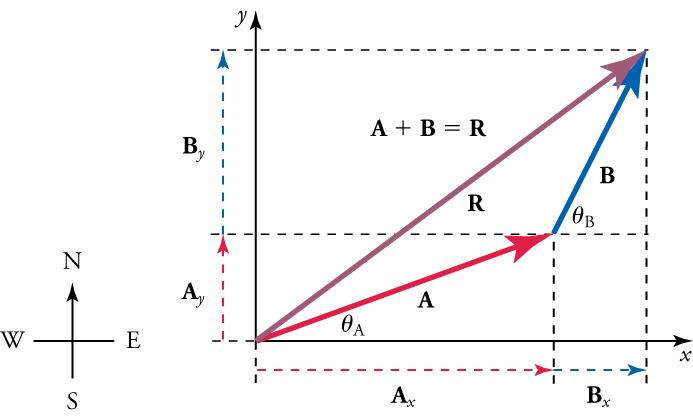
andare defined to be the components ofalong the x- and y-axes. The three vectors,,, and, form a right triangle.
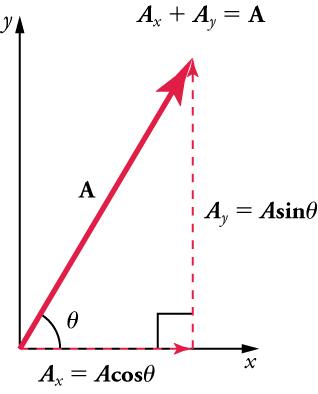
If the vectoris known, then its magnitude(its length) and its angle(its direction) are known. To findand, its x- and y-components, we use the following relationships for a right triangle:
and
whereis the magnitude of A in the x-direction,is the magnitude of A in the y-direction, andis the angle of the resultant with respect to the x-axis, as shown in Figure 5.20.
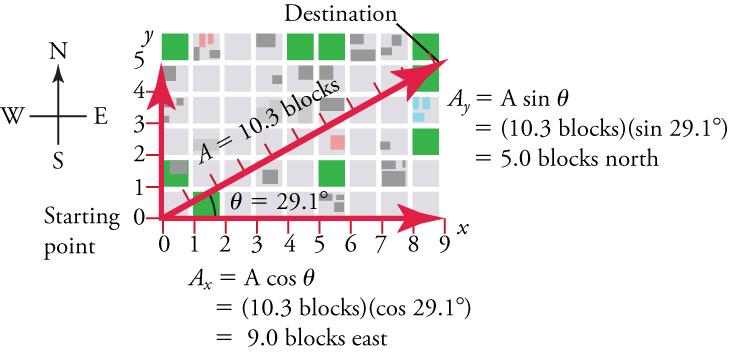
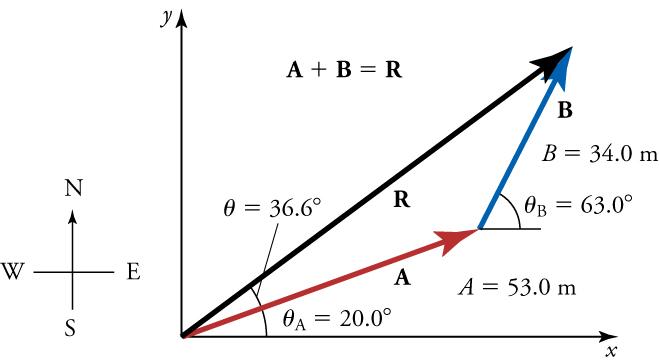
Suppose, for example, thatis the vector representing the total displacement of the person walking in a city, as illustrated in Figure 5.21.
Then A = 10.3 blocks and , so that
5.6
This magnitude indicates that the walker has traveled 9 blocks to the east—in other words, a 9-block eastward displacement. Similarly,
5.7
indicating that the walker has traveled 5 blocks to the north—a 5-block northward displacement.