A scatterplot is a graph that is used to compare two different data sets.

A scatterplot is created by rewriting the table values as a set of ordered pairs, and plotting one variable along the x-axis and one variable along the y-axis.

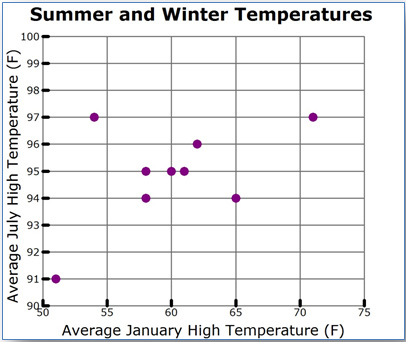
Scatterplots are typically used to determine if there is a relationship between the two variables. Researchers, engineers, and statisticians frequently use scatterplots to look for these relationships since they are a visual representation. In a scatterplot, you may spot trends that you don't easily see in a data table.

In this lesson, you will investigate ways to distinguish between different types of relationships that can be presented in a scatterplot. If the relationship is a linear one, then you will also use a trend line to make predictions.

In this section, you will compare linear and non-linear associations in order to distinguish between the two types of association in bivariate data. An association between two data sets occurs when there is a relationship between the values in one data set and the values in the other data set.

Use The ScatterPlot grapher by clicking the image below. The grapher will open in a new tab or window.

Click for additional directions on how to use the grapher.

1. The table below contains data relating the weight of an alligator in pounds to the length of an alligator in inches.

Copy the numeric portion of the data only (i.e., do not copy the row headers). Paste the data into the Data box of the grapher.

2. In the grapher, use the radio buttons to show the Light Grid Lines and change the plot type to Scatter.

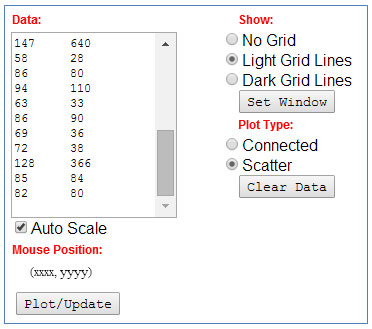
3. Click the Plot/Update button to generate a scatterplot.

See a sample graph.

4. Do the data points appear to follow a linear trend?

5. Do the data points represent a reasonably constant rate of change?

Use The Scatter Plot grapher by clicking the image below. The grapher will open in a new tab or window.

1. The table below contains data relating the length of an alligator in centimeters to the belly width of an alligator in centimeters.

   Alligator Size
   Length of Alligator (centimeters)	Belly Width of Alligator (centimeters)
   45	9
   48	10
   48	8
   50	11
   55	11
   56	13
   60	12
   62	13
   65	14
   68	14
   70	15
   72	17
   76	17
   80	18
   82	17
   84	19
   88	20
   90	21
   92	23
   94	22
   100	23
   103	23
   105	24
   107	26

   
   

   Copy the numeric portion of the data only (i.e., do not copy the row headers). Paste the data into the Data box of the grapher.

2. In the grapher, use the radio buttons to show the Light Grid Lines and change the plot type to Scatter.
   
3. Click the Plot/Update button to generate a scatterplot. Use the scatterplot to answer the questions below.
   
   See a sample graph.


4. Do the data points appear to follow a linear trend?


5. Do the data points represent a reasonably constant rate of change?

Data sets could have a linear association or a non-linear association. But not all data sets have an association. For example, consider the graph below that shows the relationship between the population according to the 2010 U.S. Census of each state and that state’s average 8th grade math score on a national mathematics test in 2013.

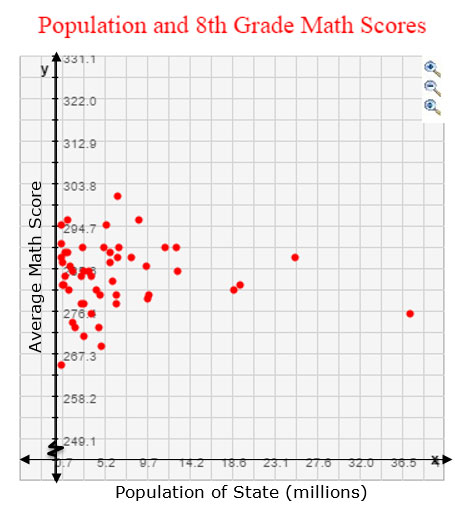
Does the data set appear to show a linear association, a non-linear association, or no association?

Pause and Reflect

1. When you look at a scatterplot of data, how can you tell the difference between the appearance of the scatterplot with a linear association or a scatterplot with a non-linear association?
2. How do the rates of change for linear associations and non-linear associations compare?

Practice

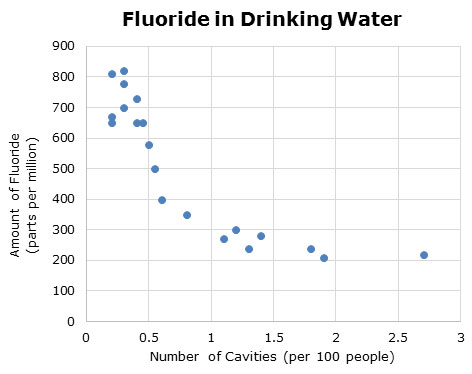
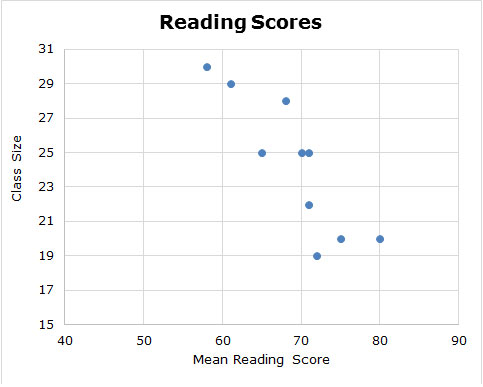
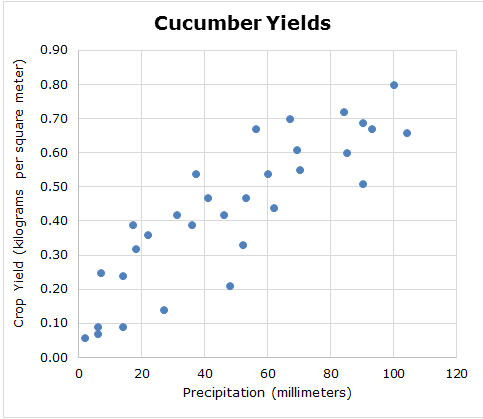
For each of the data sets below, decide whether the scatterplot best represents a linear association or non-linear association.

1. 

2. 

3. 

In the last section, you used scatterplots to distinguish between linear associations and non-linear associations. In this section, you will use scatterplots to distinguish between positive linear associations and negative linear associations. In a linear association, data will appear to be clustered around a trend line. Data are said to be clustered when the data values seem to be gathered around a particular value.

Describing Characteristics of Positive Trends
In this section, you will practice creating a scatterplot, and then use that scatterplot to analyze a relationship that exhibits a positive trend.

Use The ScatterPlot grapher by clicking the image below.

Click for additional directions on how to use the grapher.

1. The table below contains data collected twice each month regarding the number of jars of peach preserves sold at a general store in Fredericksburg, Texas, and the number of songs that are downloaded in New York City.
   

   Semi-Monthly Data Collection
   Week	Number of Jars of Peach Preserves Sold in Fredericksburg, Texas	Songs Downloaded in New York City (thousands)
   January 1	8	16
   January 15	15	35
   February 1	17	32
   February 15	11	28
   March 1	19	40
   March 15	25	55
   April 1	30	60
   April 15	31	70
   May 1	33	75
   May 15	37	80
   June 1	35	72
   June 15	32	76
   July 1	28	55
   July 15	15	33
   August 1	22	50
   August 15	24	50
   September 1	28	58
   September 15	17	40
   October 1	16	36
   October 15	8	20
   November 1	13	31
   November 15	17	35
   December 1	11	20
   December 15	15	37

Click here to open table in a new tab.

Copy the data from the Number of Jars of Peach Preserves column and Songs Downloaded column. Paste the data into the Data box of the grapher.

2.  In the grapher, use the radio buttons to show the Light Grid Lines and change the plot type to Scatter.

3. Click the Plot/Update button to generate a scatterplot. Use the scatterplot to answer the questions below.

See a sample graph.

4. Do the data points appear to follow a linear association? How can you tell?

5. As you read the graph from left to right, do the points seem to move upward or downward? 

6. As the number of jars of peach preserves sold in Fredericksburg, Texas increases, what happens to the number of songs downloaded in New York City?

7. If a greater number of jars of peach preserves are sold in Fredericksburg, what can you predict will happen to the number of songs downloaded in New York City?

8. Do you think that there is a cause-and-effect relationship between the number of jars of peach preserves sold in Fredericksburg, Texas, and the number of songs that is downloaded in New York City? Explain your answer.

9. If a trend line were found, would it have positive or negative slope?

10. Do you think that the relationship between the number of jars of peach preserves sold in Fredericksburg, Texas, and the number of songs that is downloaded in New York City has a positive or negative association? Why or why not?

Describing Characteristics of Negative Trends

Use The ScatterPlot grapher by clicking the image below.

Click for additional directions on how to use the grapher.

1. The table below contains data describing different U.S. cities’ latitude (in degrees North from the equator) and the city’s average July high temperature.
   
   

   City	Latitude (°N)	Average July High Temperature (°F)
   Atlanta, Georgia	33.75	89
   Austin, Texas	30.25	96
   Baltimore, Maryland	39.3	87
   Birmingham, Alabama	33.5	91
   Boston, Massachusetts	42.6	81
   Buffalo, New York	43	80
   Charlotte, North Carolina	35.25	89
   Chicago, Illinois	41.8	84
   Cincinnati, Ohio	39	87
   Cleveland, Ohio	41.3	83
   Columbus, Ohio	40	85
   Dallas, Texas	32.75	96
   Denver, Colorado	39.75	88
   Detroit, Michigan	42.3	83
   Hartford, Connecticut	41.8	85
   Houston, Texas	30	94
   Indianapolis, Indiana	39.75	85
   Jacksonville, Florida	30.2	92
   Kansas City, Missouri	39	90
   Louisville, Kentucky	38.25	89
   Memphis, Tennessee	35.1	92
   Milwaukee, Wisconsin	43	80
   Minneapolis, Minnesota	45	83
   Nashville, Tennessee	36.2	89
   New Orleans, Louisiana	30	91
   New York, New York	40.8	84
   Oklahoma City, Oklahoma	35.5	94
   Orlando, Florida	28.5	92
   Philadelphia, Pennsylvania	40	87
   Pittsburgh, Pennsylvania	40.5	83
   Portland, Oregon	45.5	81
   Providence, Rhode Island	41.8	83
   Raleigh, North Carolina	35.75	90
   Richmond, Virginia	37.5	90
   Riverside, California	34	95
   Rochester, New York	43.2	81
   Sacramento, California	38.6	92
   Salt Lake City, Utah	40.75	93
   San Antonio, Texas	29.5	95
   San Jose, California	37.3	82
   Seattle, Washington	47.6	76
   St. Louis, Missouri	38.6	89
   Tampa, Florida	28	90
   Virginia Beach, Virginia	36.8	87
   Washington, DC	38.8	88

Copy the data from the Latitude (°N) column and Average July High Temperature (°F) column. Paste the data into the Data box of the grapher.

2. In the grapher, use the radio buttons to show the Light Brid Lines and change the plot type to Scatter.

3. Click the Plot/Update button to generate a scatterplot. Use the scatterplot to answer the questions below.

See a sample graph.

4. Do the data points appear to follow a linear association? How can you tell?

5. As you read the graph from left to right, do the points seem to move upward or downward? 

6. As the latitude of the city increases, what happens to the city’s average July high temperature?

7. If a randomly chosen city has greater latitude, what can you predict will be that city’s average July high temperature? 

8. Do you think that there is a cause-and-effect relationship between the latitude of a city and that city's average July high temperature? Explain your answer.

9. If a trend line were found, would it have positive or negative slope?

10. Do you think that the relationship between the latitude of a city and that city's average July high temperature has a positive or negative association? Why or why not?

Pause and Reflect

1. How can you tell from a scatterplot whether a set of data shows a positive linear association or a negative linear association? (Hint: think about the slope of the line approximating the data.)
2. How could a trend line help you to determine if the slope is positive or negative?

Practice

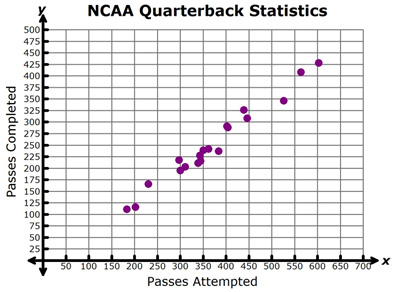
Determine whether each of the graphs below shows a positive linear association or a negative linear association.

1. 

2. 

In the last section, you studied the difference between positive linear associations and negative linear associations. Once you know that a data set has a linear association, you can use a trend line to make predictions. In this section, you will practice generating a trend line and using that trend line to make predictions from the data.

The graph below shows the relationship between the length of an alligator (in centimeters) and the belly width of an alligator (in centimeters).

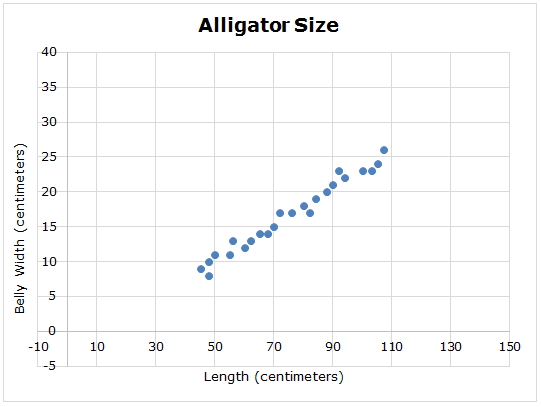
Click and drag the circles below to place a trend line on the graph. Your trend line will not connect every point, but should follow the trend in the data.

Use the trend line you estimated in the graph to answer the questions below.

1. What is the y-intercept, or starting point, of your trend line?
2. What is the approximate slope of your trend line?
3. Use your trend line to estimate the belly width of an alligator that has a length of 30 centimeters.
4. Use your trend line to estimate the length of an alligator that has a belly width of 35 centimeters.

Pause and Reflect

How does a trend line help you to make predictions from a scatterplot?

Practice

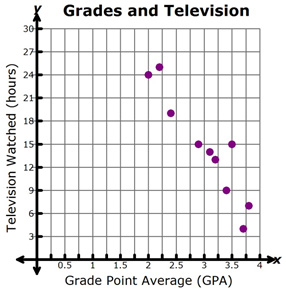
1. The graph below shows the relationship between the amount of television watched in one week and a student’s grade point average.

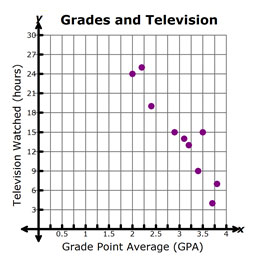
Use a trend line to estimate the grade point average a student would have if they watched 27 hours of television each week.

2. The scatterplot below shows the relationship between the sales at an ice cream store and the outdoor air temperature.

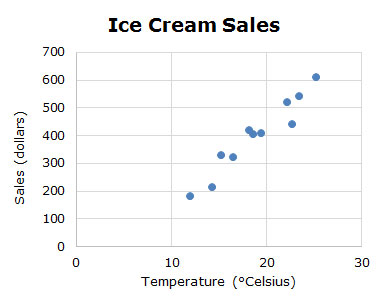
Use a trend line to estimate the temperature required for $700 in ice cream sales.

There are four types of relationships that you analyzed in this lesson.

Positive Linear Association

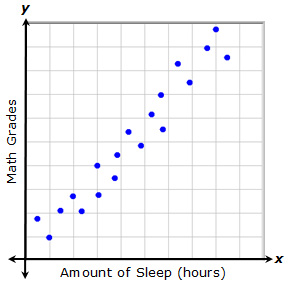
A relationship with a positive linear association is one in which both variables increase at the same time at an almost constant rate.

In this example, each point represents the amount of sleep that a student had and the grade that they received on a recent math quiz. As the amount of sleep increases, the math grade increases.

Negative Linear Association

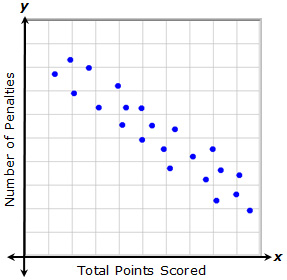
A relationship with a negative linear association is one in which as one variable increases, the other variable decreases at an almost constant rate.

In this example, each point represents the total points that a player scored and the number of penalties they received during a recent game. As the number of penalties increases, the total points scored decreases. Likewise, as the total points scored increases, the number of penalties received decreases.

Non-Linear Association

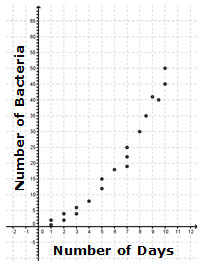
A relationship with a non-linear association is one in which as one variable increases, the other variable changes in a way that is not constant but is predictable.

In this example, as the number of days increases, the number of bacteria in a Petri dish increases. However, the number of bacteria does not increase at a constant rate, as it would for a positive linear association. Instead, the data appear to follow a curve, which is a non-linear relationship.

No Association

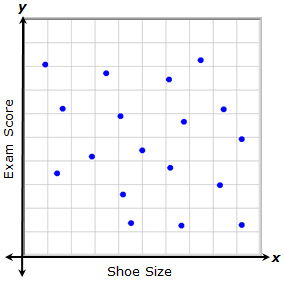
Sometimes, a relationship shows no trend. In this case, there is no detectable pattern in the data that allows you to say that as one variable changes, the second variable changes in a particular way. In this example, each point represents a student's shoe size and his or her recent social studies exam score. There does not appear to be a relationship between the shoe size and the exam score.