Introduction
Similar figures have the same shape but not necessarily the same size. You can also generate similar figures using a scale factor.
Consider the two rectangles shown below.

The angles in Rectangle 1 are congruent to the corresponding angles in Rectangle 2. After all, a rectangle contains four right angles, and all right angles are congruent. However, the sides are not congruent. Let's take a closer look at the side lengths using proportions.
Since the ratios of the corresponding side lengths are proportional, we can say that the rectangles are similar.
We can also use the ratios of corresponding sides to identify the scale factor that is used to generate Rectangle 2 from Rectangle 1.
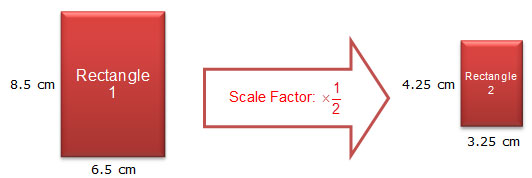
In this example, the scale factor is because the dimensions of Rectangle 1 are multiplied by to generate the dimensions of Rectangle 2.
How does this dilation affect the perimeter of the new rectangle? You will investigate that relationship.
Investigating the Perimeter of Similar Rectangles
In this section you will "build" similar rectangles with virtual toothpicks and compare their perimeters.
Use the toothpick interactive to build rectangles, and fill in the data table below the activity. You may copy the table into your notes.
Directions for rectangles you are going to build using the Toothpick Activity.
- Make sure the grid is visible (use the "Toggle Grid" button).
- Click on the box of toothpicks to add a toothpick.
- Click on a toothpick to select it.
- Click and drag with your mouse to move the toothpicks on the grid.
- Right click twice, press "r" on your keyboard twice, or click one of the "Rotate" arrows twice to rotate the toothpick vertically.
- You may use the arrow keys on your keyboard to move the toothpicks more precisely.
Below is an example of two similar rectangles created with toothpicks. This example is used to fill in the first row of the table for you. You may need to click the "Clear" button to clear the grid before constructing the larger dilated rectangles.
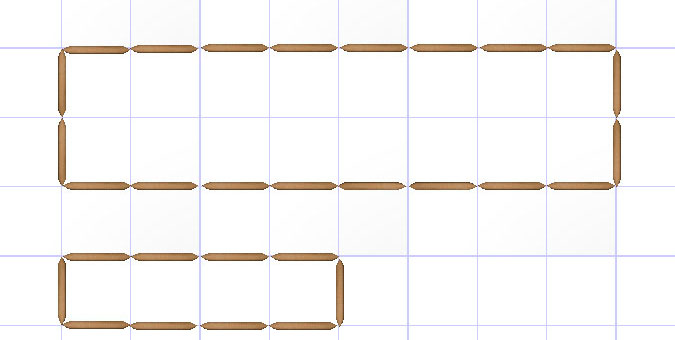
| Dimensions of Original Rectangle | Dimensions of Dilated Rectangle | Scale Factor of Dimensions | Perimeter of Original Rectangle | Perimeter of Dilated Rectangle | Scale Factor of Perimeter |
| 8 toothpicks 2 toothpicks |
4 toothpicks 1 toothpick |
20 toothpicks | 10 toothpicks | ||
| 4 toothpicks 3 toothpicks |
8 toothpicks 6 toothpicks |
||||
| 2 toothpicks 1 toothpick |
6 toothpicks 3 toothpicks |
||||
| 2 toothpicks 2 toothpicks |
8 toothpicks 8 toothpicks |
||||
| 2 toothpicks 3 toothpicks |
4 toothpicks 6 toothpicks |
What relationship do you see between the scale factor of the perimeter and the scale factor of the dimensions for each of the 5 pairs of rectangles you constructed?
Practice
1. The rectangle shown has the dimensions of feet by feet.
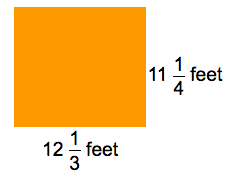
2. A civic engineer has created a model of a stop sign in the shape of a regular octagon with each side 4 inches in length.

Investigating the Circumference of Dilated Circles
Now that you have investigated with one type of polygon (rectangles), let's see if the relationship between the scale factor of a dilated polygon and the perimeter holds true for circles as well.
Recall that the perimeter of a circle is called the circumference.
Dilate the circle in the interactive below the following table to assist in the completion of the table.
- Fill in the “Radius of Dilated Circle” column.
- Make sure the black dot in the upper left hand corner is next to “Show radius.”
- Create a circle with the original radius. Note the circumference in units.
- Create a circle with the dilated radius. Note the circumference.
- Fill in the last column of the table.
|
Radius of Original Circle
|
Scale
Factor of Radii |
Radius of Dilated Circle
|
Original Circumference
|
Dilated Circumference
|
Scale Factor of Circumference
|
| 2 units |
2
|
4 units
|
12.56 units
|
25.12 units
|
2
|
| 2 units |
1.5
|
|
|
|
|
| 2 units |
0.5
|
|
|
|
|
Extra Dilations
Using the information from the table, fill in the last two rows.
|
Radius of Original Circle
|
Scale
Factor of Radii |
Radius of Dilated Circle
|
Original Circumference
|
Dilated Circumference
|
Scale Factor of Circumference
|
| 2 units |
2
|
4 units
|
12.56 units
|
25.12 units
|
2
|
| 2 units |
1.5
|
3 units
|
12.56 units
|
18.84 units
|
1.5
|
| 2 units |
0.5
|
1 unit
|
12.56 units
|
6.28 units
|
0.5
|
| 2.4 units |
1.5
|
|
|
|
|
| 2.4 units |
0.8
|
|
|
|
|
Click here to see a completed table
What relationship do you see between the scale factor of the circumference and the scale factor of the radii for each of the 5 pairs of circles you constructed?
Practice
1. A circle has a diameter of inches. If the circle is dilated by a scale factor of , what will be the effect on the circumference of the new circle?
2. A circular stepping stone used in a garden has a diameter of 18 inches. If the stepping stone is dilated by a scale factor of 1.5 to create a larger stepping stone, what will be the circumference of the new stepping stone?

Summary
To summarize what we have seen, complete the activity below. Drag the two statements that are true into the box. Leave the lie alone.