There are four important operations that you will encounter when solving problems in mathematics. The figures below indicate some of the actions in a problem that lead to different operations.

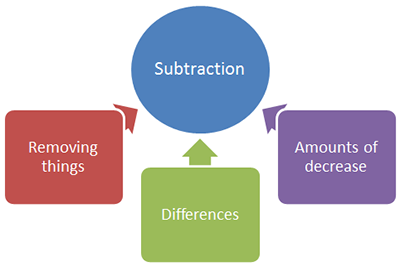
Addition and subtraction are related operations. Addition typically means to combine two or more numbers, and subtraction involves the difference, or removal, of one number from another.

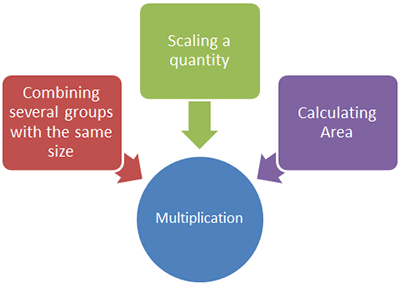
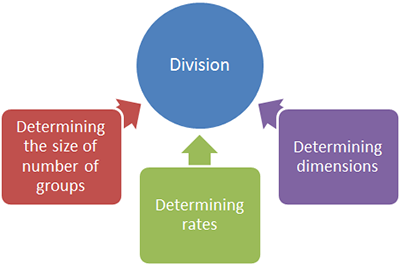
Multiplication and division are also related operations. Both operations involve grouping and rates.

You have explored how to tell when to use which operation. Now, you will focus on identifying the operation from a word problem, and then use procedures to actually perform the operation and determine a solution to the problem.

Signed numbers include integers and other rational numbers that have either a positive or a negative sign.

The sign of a number can be used to indicate a direction from a reference point, such as an elevation above or below mean sea level.

The sign of a number can also indicate a gain or a loss, such as a change in value of an asset, for example a share of stock in a corporation.

Source: Badwater Elevation Sign, Complex01 and Elevation Benchmark, Jeff Kramer, Wikimedia Commons

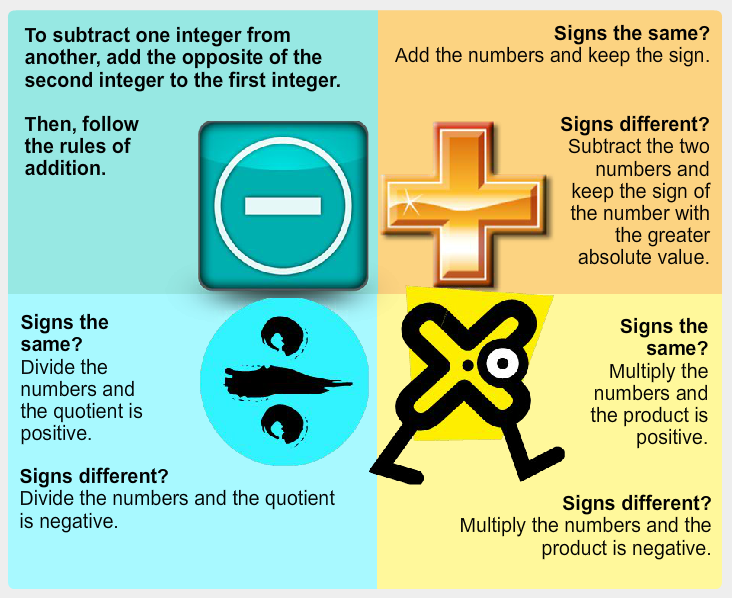
Use the diagram below to review standard procedures for adding, subtracting, multiplying, and dividing integers.

You have applied the rules of integers to solve word problems. Now, you will review ways to add and subtract decimals, and then use what you learn to solve problems relating to addition and subtraction of positive and negative decimals.

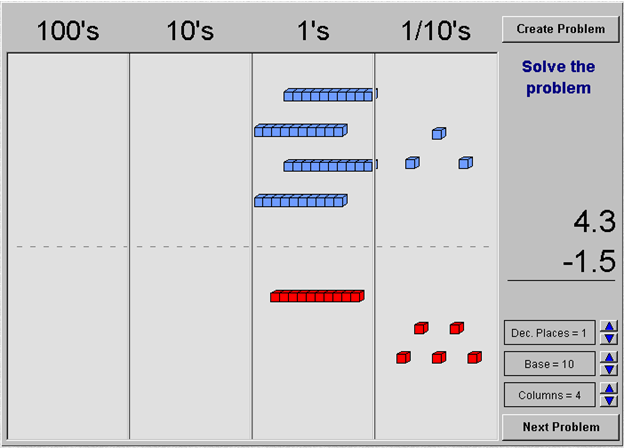
Click on the image below to open a base-ten model interactive in a new web browser tab or window. The interactive represents the two addends in an addition problem, or the minuend and subtrahend in a subtraction problem. Use the manipulative to work through at least 3 problems.

Directions

• Click on a block and drag it on top of its opposite block to remove zero pairs.
• Click on a block and drag it to the next column to regroup.
• Click “Next Problem” to move to the next problem when you are ready.

Need additional help for addition?

Need additional help for subtraction?

Use what you noticed in the interactive to answer the following questions.

In the original problem, 4.3 – 1.5, when you dragged a ones rod into the tenths column, it split into 10 tenths. How does that relate to the regrouping that was recorded symbolically in the image shown below?

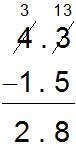
In an addition problem, such as 6.4 + 4.8, when you regroup 10 tenths into 1 one and drag the ones rod into the ones place, how did that action appear in the regrouping that was recorded symbolically such as the regrouping shown in the image below?

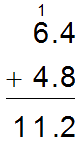
Pause and Reflect

1. Why is it important to line up the decimal point when adding or subtracting decimal numbers?

2. When regrouping 1 one and 3 tenths into 13 tenths, why do you cross out the original 3 in the tenths place and replace it with 13? 

You have used models and algorithms to add and subtract decimals, paying special attention to the regrouping that was necessary to perform the computations. Now, you will extend the idea of regrouping to models and procedures used to add and subtract fractions, including mixed numbers.

Consider the following problem.

The example below shows how Marley used fraction strips to solve this problem.

Click the image below to view additional examples, including a video with a worked-out example for you to follow.

Pause and Reflect

1. How is regrouping when subtracting mixed numbers similar to regrouping when subtracting decimals?

2. When adding decimals, you regroup when the sum of the two digits in a place value that is greater than 10. When would you need to regroup as you add mixed numbers?

Now that you’ve investigated addition and subtraction with decimals and fractions, let’s take a closer look at multiplication and division. You will start in this section with decimals, and then use a similar model to multiply and divide fractions and mixed numbers in the next section.

Consider the following problem.

1. Write an expression that you can use to determine the amount of oil that Rachel started with.
2. Anu, one student, wrote the following solution. Describe what she did to solve the problem.
   
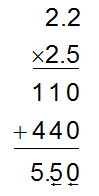
3. How would you represent 2.2 and 2.5 as improper fractions with denominators of 10?

The interactive below uses blocks to multiply decimals. When the blocks are combined, they will form a rectangle; the area of the rectangle is the product of the two decimals or the answer to Rachel’s problem.

The represents 1 unit, the represents one tenth of a unit (0.1), and the represents one hundredth of a unit (0.01).

• In the first activity, the first decimal is the length of the rectangle, and the second decimal is the width. Represent each decimal by dragging the appropriate blocks and moving them to the area for each decimal.
• In the second activity, use the information from the decimals and drag the blocks to the open area to create a rectangle. You will use the green blocks to fill in the missing pieces of the rectangle.

1. Is the answer the same as what we found earlier in Anu's solution?
2. Adjust the numerators to create and represent two more multiplication problems. Record those problems on a piece of paper.

Pause and Reflect

Based on what you saw in the interactive, why do you think that the product has the same number of digits to the right of the decimal as the total number of digits to the right of the decimal in the two factors?

In this section, you will look at models to represent multiplying and dividing fractions.

Multiplying Fractions

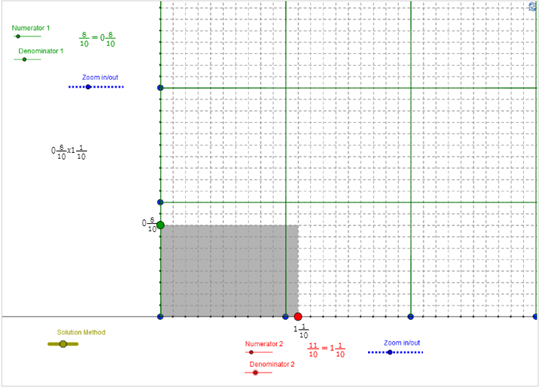
Use the interactive below to represent the problem and graphically illustrate the product. Use the Numerator and Denominator sliders to create each fraction or mixed number. You may also need to use the Zoom in/out sliders to see the entire model.

Need additional directions?

Use the interactive to answer the following questions:

1. What are the dimensions of the shaded rectangle in the solution?
   Check Your Answer


2. The solid lines represent the boundaries of a rectangle with an area of 1 square unit. The dashed lines represent the boundaries of a number of equal-sized regions within this area. What fraction of 1 does each smaller rectangle represent?
   Check Your Answer


3. Beginning with the right-hand side of the shaded region shown below, imagine moving the rectangles from the right-hand side of the shaded region shown below to the left-hand side until you fill up each unit square.
   
   
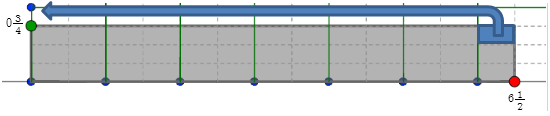
   When you have filled up all of the unit squares that you can, what would the shaded region look like?
   Check Your Answer


4. What mixed number does this rearranged figure represent? How does this compare with the product of $\frac{3}{4}$ and $6\frac{1}{2}$?
   Check Your Answer

Dividing Fractions

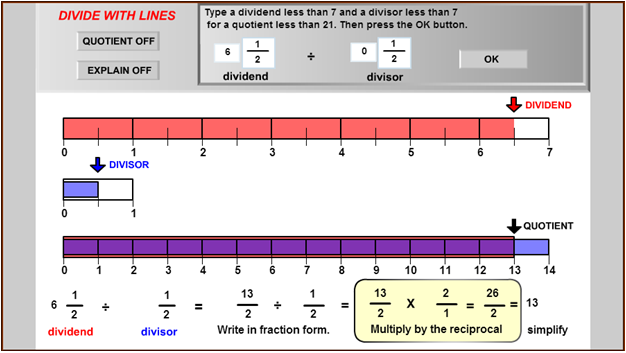
To solve this problem, Barbara used a fraction strip generator, which gave her the following diagram.

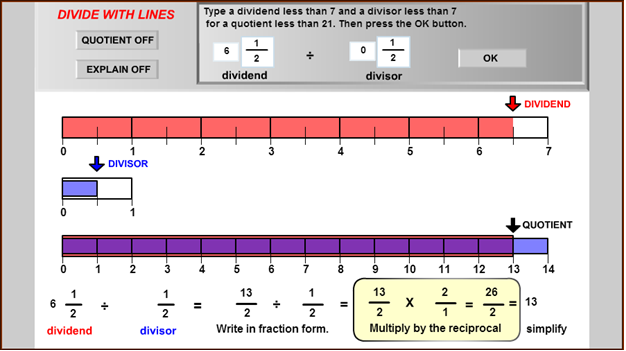
1. Barbara knew this was a division problem, not a multiplication problem. How did she know that?
   Check Your Answer


2. Use the diagram to explain why the quotient of $6\frac{1}{2}$ ÷ $\frac{1}{2}$ is 13.
   Check Your Answer

Use the same fraction strip generator that Barbara used to solve the problem below.

Click the image below to open the fraction strip generator in a new web browser tab or window. Enter the key information from the problem, including the dividend and the divisor, and then use the results to answer the questions that follow.

Need additional directions?

In the fraction diagrams, both $5\frac{3}{4}$ and $\frac{3}{8}$ are marked off into eighths. Why do you think that is the case?
Check Your Answer

To divide $5\frac{3}{4}$by $\frac{3}{8}$, the number sentence beneath the diagrams shows multiplication of $5\frac{3}{4}$by $\frac{8}{3}$, which is the reciprocal of $\frac{3}{8}$. Multiplying by $\frac{8}{3}$is the same as multiplying by $8$, and then dividing by $3$. Why do you need to multiply $5\frac{3}{4}$by $8$, which is the numerator of the reciprocal?
Check Your Answer

The next step in the number sentence divides the product of $5\frac{3}{4}$and $8$by $3$ (multiplies $5\frac{3}{4}$ by the fraction $\frac{8}{3}$). Why do you need to divide by $3$at this point?
Check Your Answer

See the completed fraction diagram for Patrice's ornament problem.

Completed fraction diagram

Pause and Reflect

1. How does the multiplication algorithm connect to the area model that you used in the first interactive?

2. How does the division algorithm connect to the fraction strip model that you used in the interactive?

You studied models that represent operations on rational numbers (fractions and decimals). You also connected those models to the standard algorithms for performing the operations.

The graphic below summarizes procedures to add, subtract, multiply, and divide decimals.

The graphic below summarizes procedures to add, subtract, multiply, or divide fractions, including mixed numbers.