Introduction
In the United States, the American System of Measure is used. The concepts of the inch, mile, gallon, pound, ounce, and even degrees Fahrenheit are commonplace in our everyday lives. These are referred to as customary units. While all countries have adopted the metric system, including the United States, customary units are still used throughout the world. In the United States, the National Institute of Standards and Technology defines U.S. customary units. Many other countries that are former British colonies also use variations of Imperial or English units of measure.
Source: The Red Hat of Patrick Ferrick, The British Empire, Wikimedia Commons

Almost all of the other countries in the world adopt and use the International System of Measure, or metric system, when measuring and describing length, capacity, volume, mass, weight, and temperature. Although there have been past political efforts to convert the United States to the use the metric system, there has never been a mandate to change our customary units of measure.
However, there are several industries in the United States that rely on the metric system in order to communicate globally. This means that it is absolutely necessary for us to be able to convert efficiently and accurately between the measurement systems.
What are some of the industries in the United States, particularly in Texas, for which the metric system might be used?
Sources for images used in this section:
Shelby AC Cobra, Jaydec, Wikimedia
Medical Researcher, Hannes Grobe, Wikimedia
Laboratory Equipment, Dobrzejest, Wikimedia
Converting Units of Length
In the customary measurements of lengths, there are several units that are used, but the inch is the smallest unit of measure.
Fill in the chart below for customary units.
Similarly, the metric system has several units that are used, but the meter is the most basic unit of measure. Metric prefixes, such as centi- and kilo- are used to indicate larger or smaller units of measure in the metric system.
Fill in the chart below for metric units.
Copy the information from the two activities you completed into your notes.
Consider the following problem situation.
 Sean has been training for a bike race. He knows that the race he will be competing in will be 41 kilometers in distance, so he has been riding 25 miles each day in order to train for the race. Have Sean's training rides been at or beyond the distance of the race?
Sean has been training for a bike race. He knows that the race he will be competing in will be 41 kilometers in distance, so he has been riding 25 miles each day in order to train for the race. Have Sean's training rides been at or beyond the distance of the race?
To answer this question, you will need to recall one fact of converting between customary and metric systems: 1 inch = 2.54 cm. Depending on the direction in which you are converting, this fact gives you a rate of conversion as either 1 inch for every 2.54 centimeters or 2.54 centimeters for every inch. Before you answer Sean's question, look at the relationship of 1 inch = 2.54 cm a little more closely.
Specifically, look at the conversion of customary to metric using 1 inch = 2.54 cm. If you had 10 feet and wanted to find out how many meters that would be, you would need to find out how many inches would be in 10 feet. Convert each inch to 2.54 cm. Finally, convert centimeters to meters. Let's examine this process in more detail.
One way to perform unit conversions mathematically is to use a method called dimensional analysis. In dimensional analysis, conversions are represented as unit rates and are positioned such that the numerators and denominators will cancel. Dimensional analysis works because the unit rate is technically the same quantity in both the numerator and denominator, which is equal to 1.
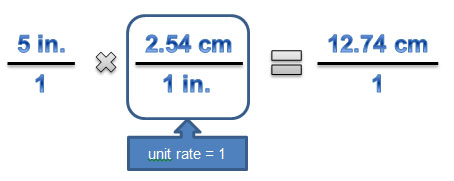
Click on the link to access an applet that can be used to perform unit calculations. (Note: Use either Firefox or Internet Explorer as your browser in order to access the applet.)
Watch this video to see how one math tutor explains the process of using dimensional analysis to convert 10 feet into meters.
Using this same process, let's answer Sean's question.
Sean has been training for a bike race. He knows that the race he will be competing in will be 41 kilometers in distance, so he has been riding 25 miles each day in order to train for the race. Have Sean's training rides been at or beyond the distance of the race?
First, make a plan for converting the units from miles to kilometers.
Click on the image below to access the applet. Use the applet to perform dimensional analysis in order to perform the conversion.
After you have finished your conversion and justified your answer, watch this video to see another student’s solution.
(NOTE: Use either Firefox or Mozilla as your browser in order to access the applet.)
Pause and Reflect
1. How is dimensional analysis similar to multiplying fractions that have common factors?
2. Why does a common unit in the numerator and in the denominator cancel when using dimensional analysis?
Converting Units of Capacity and Volume
Just like you did with units of length, you can use dimensional analysis to convert units of capacity and volume. As mentioned in the first section of this lesson, medicine and science are two of the primary reasons that the United States must convert between the two systems of measure. This is especially true for volume and capacity.
To move forward with conversions, let’s first review customary and metric units of volume and capacity.
Copy the information from the activity into your notes.
In the metric system, the most basic unit of volume is the liter. However, the liter is technically not an SI unit of measure, but it is considered to be a metric unit. The SI system uses cubic meters as a unit of volume, and a liter is defined as 1000 cubic centimeters. SI prefixes, such as milli- and kilo- are commonly used with liters. In medicine, a common metric/SI unit of volume or capacity is the cubic centimeter, or cc.
The fluid ounce in the customary system is the smallest unit, but this fluid ounce is much different than the ounce used in measuring weight. This is due to the fact that the fluid ounce measures volume, which refers to the amount of space a given object displaces, whereas the ounce simply measures weight.
Once again, just as 1 inch = 2.54 centimeters was the key in converting between the two systems, the conversion factor you must know for volume and capacity is that 1 fluid ounce (fl. oz.) = 29.6 milliliters (mL) or 1 fluid ounce (fl. oz.) = 29.6 cubic centimeters (cc).
 Consider the following problem situation.
Consider the following problem situation.
Raul reads that the human body contains about 5.6 liters of blood. About how many quarts of blood does the human body contain?
First, make a plan for converting the units from liters to quarts.
Click on the image below to access the applet. Use the applet to use dimensional analysis in order to perform the conversion.
(NOTE: Use either Firefox or Internet Explorer as your browser in order to access the applet.)
Pause and Reflect
How is converting units of capacity or volume with dimensional analysis similar to converting units of length?
Converting Units of Mass and Weight
Another common conversion between measurement systems deals with mass and weight. Mass is the amount of matter that an object contains, and weight is the force exerted on this amount of matter by gravity. Customary units describe an object’s weight, and metric/SI units describe an object’s mass. Weight and mass conversions occur in fields such as medicine, construction, and shipping, especially since these fields tend to cross international boundaries quite frequently. In order to convert between systems, you must first identify key units of measurement for mass and weight in each measurement system.
Copy the information from the activity into your notes.

There are two important conversion facts that can be used to convert mass and weight between systems: 1 pound (lb) = 454 grams (g) and 1 kilogram (kg) = 2.2 pounds (lbs).
To use these facts in a problem situation, consider the following report.
In September 2009, the car manufacturer Ferrari introduced the Ferrari 458 Italia sports car. The engineering and specifications of this machine were impressive to sports car fans, but since it was a European model, its mass is reported as 1,485 kg. What is the weight of this sports car in pounds?
First, make a plan for converting the units from kilograms to pounds.

Source: Ferrari 458 Italia, Aurélien Vialatte, Wikimedia
Click on the image below to access the applet. Use the applet to perform dimensional analysis in order to perform the conversion.
(NOTE: Use either Firefox or Internet Explorer as your browser in order to access the applet.)
Pause and Reflect
Why is it important to be able to convert weight in pounds to mass in kilograms or vice versa?
Problems with Multiple Unit Conversions
At certain points, there will be a need to convert between measurement systems when there are multiple units and types of measurements being used to describe an object or process. Usually, these types of problems involve rates.
steel mill worker
 For example, in describing the density of steel using customary units, you would say that the density of steel is 490 pounds per cubic foot . However, most manufacturers of steel, as well as the machinery used in the process, rate the density of steel using the metric system. This is because steel is manufactured and shipped all over the world.
For example, in describing the density of steel using customary units, you would say that the density of steel is 490 pounds per cubic foot . However, most manufacturers of steel, as well as the machinery used in the process, rate the density of steel using the metric system. This is because steel is manufactured and shipped all over the world.
Knowing that the density of steel in customary units is ,
what is the density of steel in grams per cubic centimeter ?
1. Does this problem require you to convert from metric/SI units to customary units or from customary units to metric/SI units?
2. Which units will you be converting in this problem?
In this situation, you are combining mass/weight and volume measurements, which means that you will need the following two important conversion factors:
1 pound (lb) = 454 grams (g)
1 cubic inch (in.3) = 16.4 cubic centimeters (cm3)
Just as you have done before, you will need to write out a plan to follow for the unit conversion. There are two distinct conversions that you will perform; however, let's work on them simultaneously. Be sure to note where your units are in the fraction (numerator or denominator) and cancel them out so that you are left with grams per cubic centimeter.
What is your plan to perform the unit conversions?
Click on the image below to access the applet. Use the applet to perform dimensional analysis in order to perform the conversion.
Watch this video to check your answer.
(NOTE: Use either Firefox or Mozilla as your browser in order to access the applet.)
Pause and Reflect
How does unit conversion for rates compare with unit conversion for quantities?
Summary
In summary, you investigated different ways to use dimensional analysis in order to solve problems that require you to convert measurement units between U.S. customary units and metric/SI units.
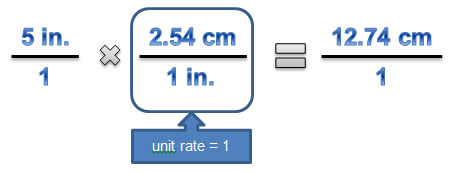
Dimensional analysis works because you multiply a given quantity times a unit rate that is equal to 1. In the equation above, 2.54 centimeters = 1 inch, so the ratio of these two quantities is 1. To convert 5 inches to centimeters, you can multiply 5 inches by “1,” but the “1” is disguised as a unit rate.
While people in the United States primarily rely on customary units (you buy gasoline by the gallon, apples by the pound, and mail letters by the ounce), people in most other countries use metric/SI units. Because so many industries are now global, it is important to be able to convert between customary units and metric/SI units.