Introduction
Recall that similar figures have the same shape but not necessarily the same size. You can also generate similar figures using a scale factor.
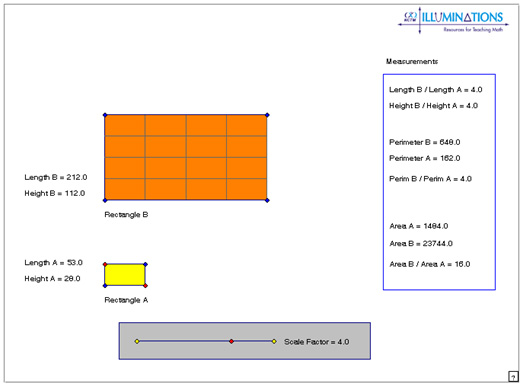
Consider the two rectangles shown below.

The angles in Rectangle 1 are congruent to the corresponding angles in Rectangle 2. After all, a rectangle contains four right angles, and all right angles are congruent. However, the sides are not congruent. Let's take a closer look at the side lengths using proportions.
Since the ratios of the corresponding side lengths are proportional, we can say that the rectangles are similar.
We can also use the ratios of corresponding sides to identify the scale factor that is used to generate Rectangle 2 from Rectangle 1.

In this example, the scale factor is because the dimensions of Rectangle 1 are multiplied by to generate the dimensions of Rectangle 2.
How does this dilation affect the area of the new rectangle? You will investigate that relationship.
Investigating the Area of Similar Rectangles
In this section, you will use an interactive applet to build a series of rectangles.
Click the image below to open an applet to investigate how using a scale factor affects the area of similar rectangles. Use the applet to complete the table below, and then use your table to answer the questions that follow.
Click here for directions to use the applet.
|
Length A |
Height A |
Scale Factor |
Number of Rectangle A inside Rectangle B |
Length B over Length A Length B Length A |
Height B over Height A Height B Height A |
Area B over Area A Area B Area A |
|
53 |
28 |
4 |
16 |
4 |
4 |
16 |
|
53 |
28 |
3 |
|
|
|
|
|
53 |
28 |
5 |
|
|
|
|
|
19 |
38 |
3 |
|
|
|
|
|
35 |
38 |
3 |
|
|
|
|
|
35 |
45 |
3 |
|
|
|
|
- How does the Scale Factor compare to the ratio ?
- How does the Scale Factor compare to the ratio ?
- How does the Scale Factor compare to the ratio ?
- How does the Number of Rectangle A’s that appear to fit inside Rectangle B compare to the Scale Factor?
- Is the relationship you have observed between the ratio and the Scale Factor true for different scale factors? How do you know? Confirm your answer using additional scale factors for the same Rectangle A in the applet.
- Is the relationship you have observed between the ratio and the Scale Factor true for different combinations of lengths and widths? How do you know?
Practice
1. Rectangle QUAD is dilated by the scale factors shown. Identify the changes in the area of Rectangle QUAD that will result from the dilation.
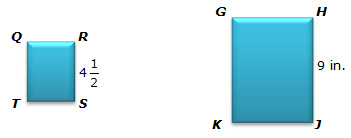
2. Rectangle QRST is similar to rectangle GHJK. If the area of rectangle QRST is square inches, what is the area of rectangle GHJK?
Investigating the Area of Similar Polygons and Circles
Now that you have investigated one type of polygon (rectangles), let's see if the relationship between the scale factor of a dilated polygon and the area holds true for other polygons and circles as well.
Recall that the perimeter of a circle is called the circumference.
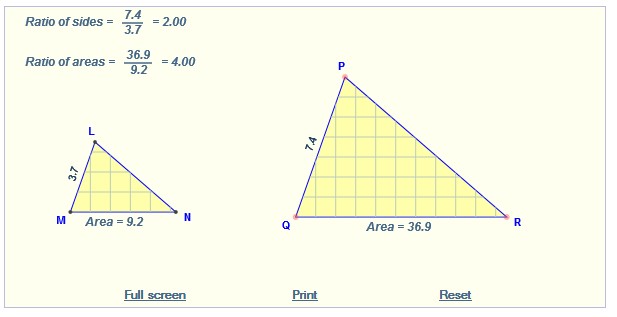
Click on the image below to access an activity with similar triangles. Move any point on ΔPQR to dilate it. The scale is located in the upper left hand corner. (Remember from the first section that the scale factor is the ratio of corresponding sides.) Notice how the dilated area and the ratio of areas change. Fill in the following chart.
|
Area of ΔLMN |
Scale Factor |
Area of ΔPQR |
(Scale Factor)2 |
Area of ΔLMN × (Scale Factor)2 |
|
9.2 |
3 |
83.1* |
9 |
82.8* |
|
9.2 |
2 |
|
|
|
|
9.2 |
1.5 |
|
|
|
|
9.2 |
0.75 |
|
|
|
|
9.2 |
0.5 |
|
|
|
*The answers are close; the applet rounds creating a slight difference.
Click here to see a completed table.
What is the relationship between the area of ΔLMN, the scale factor, and the area of ΔPQR?
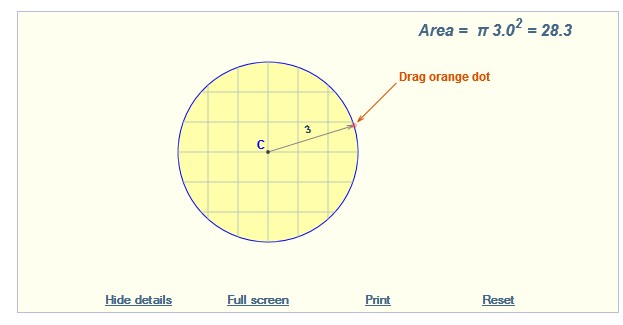
Click on the image below to see an activity that will find the area of a circle. By changing the radius (moving the orange dot), the circle dilates. Use the activity to complete the following table. Start with a circle with a radius of 1.
|
Area of Original Circle |
Scale Factor |
Area of Dilated Circle |
(Scale Factor)2 |
Area of Original Circle × (Scale Factor)2 |
|
3.1 |
3 |
28.3* |
9 |
27.9* |
|
3.1 |
2 |
|
|
|
|
3.1 |
2.6 |
|
|
|
|
3.1 |
1.8 |
|
|
|
|
3.1 |
1.5 |
|
|
|
*The answers are close; the applet rounds creating a slight difference.
Click here to see a completed table.
What is the relationship between the area of the original circle, the scale factor, and the area of the dilated circle?
Practice
1. A circle has a diameter of inches. If the circle is dilated by a scale factor of , what will be the effect on the area of the new circle?
2. A masonry crew is laying a garden feature made out of bricks that are in the shape of an equilateral triangle. The area of each brick is 4 square inches. The finished floor is a similar triangle that is dilated by a scale factor of 16. What is the area of the finished floor?