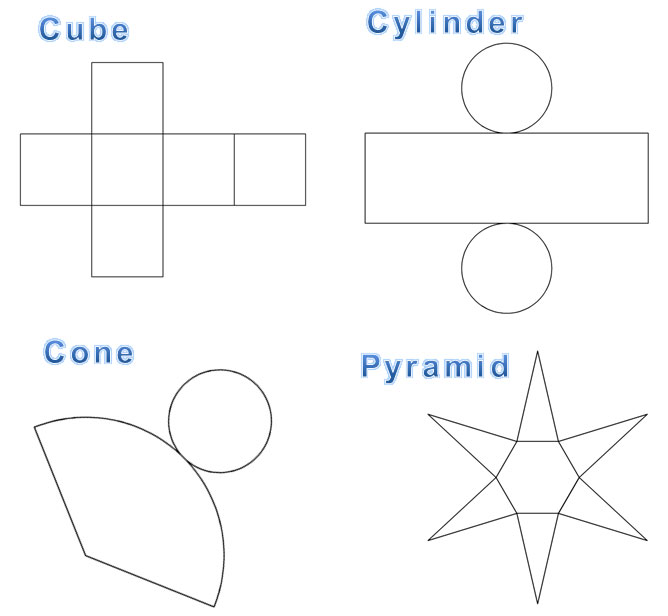
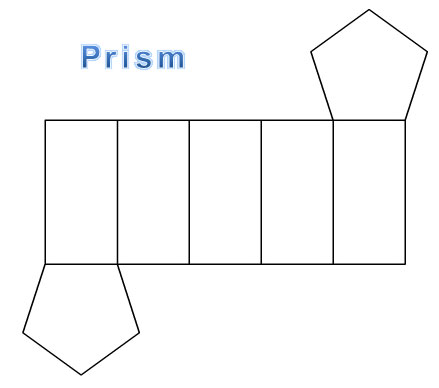
Introduction
A net is a two-dimensional representation of a three-dimensional figure that is unfolded along its edges so that each face of the figure is shown in two dimensions.
Consider the rectangular prism shown.
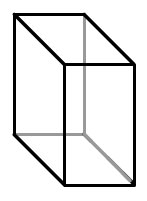
Consider how the net below will fold to create the prism.
The example shown above is a polyhedron.
In a previous lesson, you discovered Euler's Theorem for the relationship among vertices, faces, and edges of three-dimensional solids.
In that same lesson, you worked through conjectures about three-dimensional solids. Now, you will use the information that you learned from that lesson and begin working with the nets of three-dimensional solids.
Attributes of Nets and Polyhedra—Faces, Edges, and Vertices
Although polyhedra are generally named by the number of faces that make up the figure, it is common to see qualifier of the face shape within the name.
Likewise, in naming three-dimensional figures that are not regular polyhedron, it is critical to know the shape of the base. The name of the shape of the base will be used in naming the solid and the net of the solid.

Euler’s Theorem tells us the relationship between the number of faces, edges, and vertices in any polyhedron. Remember that a polyhedron is a three-dimensional figure whose faces are all polygons, and polygons are planar shapes with closed edges and no curved edges.

Source: Leonhard Euler, Jakob Emmanuel Handmann, Wikimedia Commons
Will Euler’s Theorem still apply to a polyhedron that is not regular?
 |
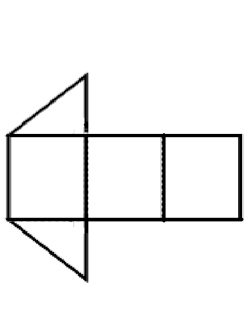 |
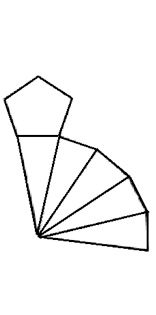 |
Look at the table below to see information about each polyhedron.
| Name of Shape | Number of Vertices | Number of Faces | Number of Edges | Check V+F – E = 2 |
| Pentagonal Prism |
10
|
7
|
15
|
10 + 7 – 15 = 2 |
| Triangular Prism |
6
|
5
|
9
|
6 + 5 – 9 = 2 |
| Pentagonal Prism |
6
|
6
|
10
|
6 + 6 – 10 = 2 |
Conclusion Questions
- Why do you think Euler’s Theorem still applies to polyhedra that are not regular?
- To what nets of three-dimensional figures, if any, will Euler’s Theorem not apply?
|
Pause and Reflect How does using a net help you to visually recognize faces, edges, and vertices of a three-dimensional figure? |
Practice
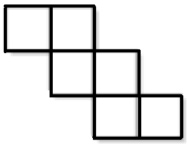
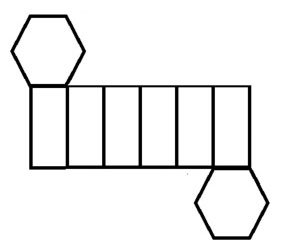
1. What 3-D figure will the net below make when it is folded?
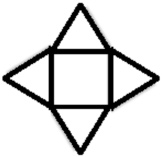
2. For the figure whose net is shown below, identify the figure, the number of faces, the number of edges, and the number of vertices.
3. Sheila constructed the net shown below. How many faces, edges, and vertices does the three-dimensional figure represented by the net have?
Nets of Cones and Cylinders
Although Euler's Theorem does not apply when describing the attributes of the nets of cylinders and cones, there are some special relationships. However, these relationships will become more apparent once you begin to use nets in the application of measuring solids.
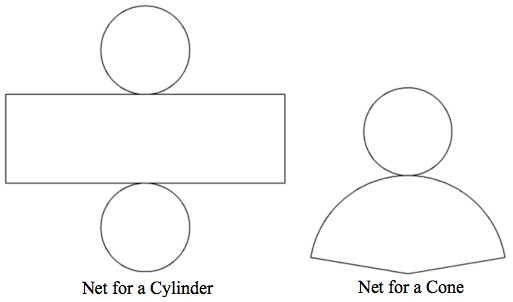
Questions
- What shapes do the nets of a cylinder and a cone have in common?
- Are all of the shapes shown in the nets polygons? How can you tell?
- A face is a polygonal region on the surface of a three-dimensional figure. Do cylinders and cones have faces? Why or why not?
| Pause and Reflect
An edge is the intersection of two or more faces, and a vertex is the intersection of two or more edges. Do cylinders or cones have edges and vertices? How do you know? The peak of a cone is sometimes called an apex or a vertex of the cone. How is this vertex like vertices in polyhedra? How is it different? |
Applying Nets—Surface Area
In this section, you will use nets to determine the surface area of a given figure.
Part 1: Surface Area of Cones
Let’s use the net of a cone to help us measure and describe three-dimensional figures in terms of exterior (surface area) and capacity (volume).
Based on the net of the cone that we looked at in the previous section, let’s see how the net can help derive the formula to find the surface area for the cone.
The video below shows the source of the formula for the surface area of a cone and how it relates to the net of the cone.
*The reference in this video to the state assessment is outdated.
Find the total surface area of the net of a cone with the height of four centimeters and a radius of three centimeters. Compare your work with the student work sample below.
Part II: Surface Area of Prisms
Finding the surface area of a prism from its net is not as difficult as using the net of a cone.
China's National Aquatic Centre or "Water Cube" that was used in the 2008 Beijing Olympics serves as a good example. Although the building itself is a complex hexahedron, the net of a rectangular prism can be helpful in determining the surface area of the building. Click here to see an animation.
Given the approximate dimensions in the net of the Water Cube, what is the surface area of the exposed faces (faces that you would see if you were looking at the actual building)?
|
Pause and Reflect How does a net help you to determine the surface area of a three-dimensional figure? |
Applying Nets—Volume
In the last section, you used nets to represent three-dimensional figures and determine the surface area of those figures. In this section, you will use nets to represent three-dimensional figures and determine the volume of those figures.
Knowing that volume is measuring the capacity of a three-dimensional shape, the net of the shape is very helpful in finding the volume.
In the volume formula, V = Bh, what do B and h stand for?
Use the information in the interactive you just completed to answer the following questions.
- How did you calculate the height of the cone from the slant height?
- How are the volume formulas for the cone and the cylinder different?
Practice
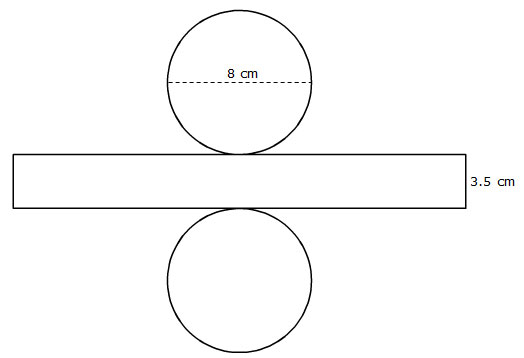
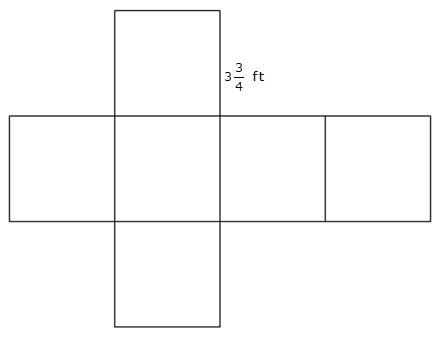
Use the nets shown to calculate the volume of the figures they represent.
1. Cylinder
2. Cube
Summary
In this lesson, you used nets of three-dimensional figures in order to make conjectures and draw conclusions about the figures. You compared the numbers of faces, edges, and vertices, as well as used nets to calculate surface area and volume of the three-dimensional figure represented by the net.
Some common nets that you may see are shown below.