Solving Proportional Relationships by Multiplying by a Constant
In this resource, we will look more closely at one method for solving problems that involve proportional relationships—multiplication by a constant.
Read the following problem and answer the questions below. Record your answers on a separate piece of paper or using your notes. 
A man is planning to grow chili peppers in his garden. He knows that each plant will produce eight chili peppers. He wants to know how many peppers he will grow based on the number of plants.
Copy the following table into your notes and fill in the missing information.
|
Plants
|
Process
|
Peppers
|
|
1
|
1(8)
|
8
|
|
2
|
2(8)
|
16
|
|
3
|
|
|
|
4
|
|
|
|
5
|
|
|
|
8
|
|
|
|
10
|
|
|
Click here to see the completed table.
1. What do all the expressions in the 'Process' column have in common?
2. Write a rule for determining the number of peppers, if you know the number of plants.
3. Now write your rule as an equation. Since both "peppers" and "plants" start with the letter p, you will have to use different letters for your variables. In your equation, use y for the number of peppers and x for the number of plants.
In this problem we solved a proportional relationship by multiplying by a constant:

Instead of writing out the word "constant," mathematicians use the letter k.
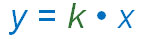
The constant that you use does not have to be a whole number. It can be any number including fractions, decimals, percents, or irrational numbers like √2.

On track and field day at an elementary school, the teacher wants to give her class a treat, so she buys popsicles. The popsicles cost $0.45 each. Fill in the following table to determine the equation for the cost c, of buying p, popsicles.
|
Popsicles
|
Process
|
Cost
|
|
1
|
1(0.45)
|
$0.45
|
|
2
|
||
|
3
|
||
|
5
|
||
|
10
|
||
|
p
|
Click here to see the completed table.
1. What is the rule for filling in the table?
2. What is the constant in this problem?
3. Write an equation that could be used to solve this problem.
4. The teacher has 22 students, how much will she pay for the popsicles?
Both of these problems could be modeled using proportional relationships because when one variable changed, the other changes by the same factor. We solved them by finding a constant of proportionality between the two variables and set up the equation y = constant • x. The equation may also be written in the form, y = kx where k represents the constant of proportionality.
Unit Rate
In section 1, we learned about solving proportional relationships by multiplying by a constant. In this section, we are going to focus on a special kind of number for the constant called the unit rate. A unit rate is a ratio in which one of the values being compared is 1. Some common unit rates are miles (or kilometers) per hour, wages earned per month, meters per second, cost per item, and miles per gallon.
1. What do you notice about the list of common unit rates?
2. Which mathematical operation is implied by the word, "per?"
3. Which mathematical operation would you use to find a unit rate from information given in a problem?
Copy the following table in your notes and fill in the missing information.
|
Situation |
Rate |
Unit Rate |
||
|
Juan is training to run a long-distance race. While he trains, he keeps track of his pace in minutes per mile. On one of his training runs, he takes 36 minutes to run 4.5 miles. |
36 minutes |
Per |
4.5 miles |
8 min/mile |
|
Maria's dad put 7 gallons of gas in the car for $24.50. What was the price per gallon? |
|
Per |
|
|
|
Linda is filling out an application for a job. One of the questions on the application asks her how much she made per month at her last job. In her last job as a babysitter, she made $600 in 4 months. |
|
Per |
|
|
|
Mike reads a 495 page book for homework. It took him 15 days to finish the book. How many pages did he read per day? |
|
Per |
|
|
Click here to see the completed table.
You want to pay careful attention to the units when you set up your equation.
The unit rate for the first situation is 8 min/mile. We can write this as
What happens when you multiply by a time of five minutes?
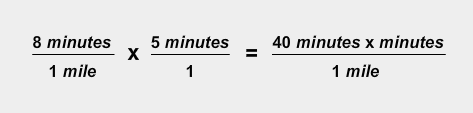
What happens when you multiply by a distance of five miles?

1. Does this answer make sense?
2. What has to be true about the units to be sure that your equation is correct?
3. Take another look at the first situation in the top row of the table. Write an equation that you could use to calculate m, the number of minutes Juan runs if you know d, the distance he covers in miles. Assume that he keeps the same pace.
4. If the race is 3.1 miles long, how long will it take Juan to finish it?
5. Now consider the third situation with Linda and her babysitting. Write an equation that Linda could use to calculate p, the pay that Linda could expect if she were to continue babysitting for m months.
6. Linda decides not to take the new job and continues babysitting, how much will she earn in 7 months?
Converting Between Systems of Measurement
Another special kind of constant that can be used in solving problems involving multiplication is called a "conversion constant." A conversion constant is used to convert from one system of measurement to another.
For example, there are 1.61 kilometers in every mile. How would we write an equation that you could use to calculate d, the number of kilometers in m miles?
First, we need to take a closer look at the conversion factor, "There are 1.61 kilometers in every mile."
1. What units are in the denominator?
2. Do we want to multiply this conversion factor by d, kilometers or by m, miles?
3. How should we write the equation that calculates the number of kilometers in m miles?
4. Write the equation in your notes and then click on the "d" to check your answer.
Write the equation in your notes.
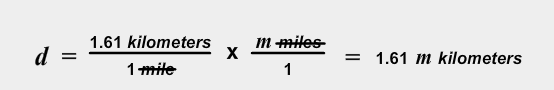
How many kilometers are in 6 miles?

Try another example.

You are making a cake to surprise your mom for her birthday. You look online and find a recipe for her favorite cake, but the units are all metric. The recipe calls for 0.30 liters of milk and all you have is a measuring cup. Luckily, you have your science textbook with you at home, and there is a table in the back of conversion factors. The table says that there are 4.23 cups in one liter.
1. Write this conversion factor as a ratio of cups to liters.
2. What units are in the denominator?
3. Do you want to multiply this conversion factor by cups or by liters to make the units cancel?
Write the equation in your notes.
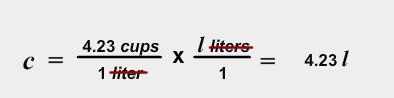
How many cups are there in 0.30 liters of milk?
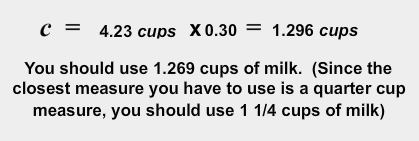
Percent Problem
Percent problems may be solved using several different methods. One method uses multiplication by a constant factor. Work through the examples below to examine the constant factor method as well as a few other methods.
Try the following two examples.

Example 1
Freddie is downloading a program that is 1.5 megabytes. According to the progress bar, it has finished 30% of the download. How many megabytes have been downloaded so far?
On a separate piece of paper, draw a percent bar that represents how you would use a percent bar to find the amount of data that has been downloaded so far.
1. What does the problem give you?
2. What does the problem ask for?
Click here to see an example of a percent bar.
Try solving the problem using a proportion.
Copy the following table into your notes and fill in the missing information:
|
Percent |
megabytes |
|
|
Part |
|
m |
|
Whole |
100 |
|
Click here to see the completed table.
1. Use the chart to set up a proportion relating the percent to the number of megabytes.
2. Use this proportion to find m, the number of megabytes downloaded so far.
3. Finally, let's try the same problem by using an equation. What is your plan to solve the equation?
4. Write your plan as an equation.
5. How many megabytes have been downloaded?

Example 2
You want to buy a television in an electronics store that offers a payment plan so that you can make payments every month instead of paying all at once. To qualify for the payment plan, the store requires you to make a 20% payment today.
If the television originally cost $1100, how much do you need to pay today?
Click here to see the percent bar.
Use each of the methods described below to solve this problem then click to check your answer.
1. Create a data table and use it to write a proportion relating the percent to the price you need to pay today.
2. Write and solve an equation that you could use to solve for the p, the payment you need today if the television has an original cost of c dollars.
When solving equations in the form of y = kx, multiplying by a percent will help you find a part of the larger whole.
Practice
In this resource, we practiced solving proportional relationships by multiplying by a constant, and we covered three special cases.
|
Unit rate—a ratio where the denominator is 1 |
 |
 |
Conversion factors—a way to convert from one system of measurement to another |
|
Percent problems—finding a part of a whole by multiplying by a percent |
 |
Solve the following sample problems.

Example 1
1. Mike is driving on the highway at a rate of 65 miles per hour. Write an equation that you could use to solve for d, the distance he drives in h hours.
2. How far would Mike drive in 7 hours at this speed?
 Example 2
Example 2
A mechanic is working on the engine of a car that is stalled on the side of the road. The mechanic needs to remove a bolt to get to the part of the engine that is broken. The bolt head is marked in inches, but the mechanic only brought his wrench set that is marked in millimeters. There are 25.4 millimeters in one inch.
1. Write an equation that the mechanic could use to calculate w, the correct wrench size in millimeters given b, the bolt size in inches.
2. What size wrench would be most appropriate to remove a 3/4 inch bolt?
 Example 3
Example 3
A music store is having a clearance sale, and everything in the store is 40% off.
1. Write an equation that you could use to find d, the amount that is being discounted from an item that costs c dollars.
2. How much will be discounted from a $575 dollar guitar?