Introduction
In this resource, you will focus on using ratios and proportions to solve problems involving similar figures. To do so, let's review some important terminology before beginning an investigation.
An enlargement is a dilation that results in a larger figure.
A reduction is a dilation that results in a smaller figure.
Similar Figures and Scale Factor
In the geometry sketch below, quadrilateral ABCD is dilated about point E using the scale factor identified in the ScaleFactor slider bar. The resulting quadrilateral, A'B'C'D', is shown.
Generating Similar Figures
Click on the image below to adjust the size of Quadrilateral A'B'C'D'.
OnTRACK for College Readiness, 11 April 2014, Created with GeoGebra
Use the interactive geometry sketch to generate several different values, and then complete the table shown below.
|
Length of BC |
Scale Factor |
Length of BC × |
Length of B'C' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Click here to see a sample table.
How are the length of BC, the Scale Factor, and the length of B'C' related?
Use the patterns that you have observed to predict the length of A'D' for the following scale factors:
|
Length of AD |
Scale Factor |
Length of A'D' |
|
2 |
2.5 |
|
|
2 |
1.8 |
|
|
2 |
1.2 |
|
|
2 |
0.6 |
|
Practice
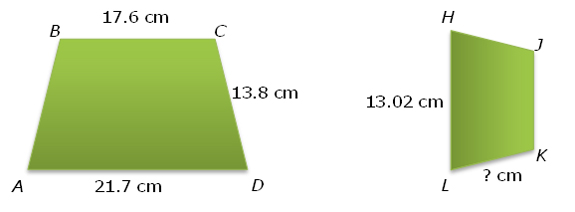
- Trapezoid ABCD is similar to trapezoid HJKL. What is the length of KL?
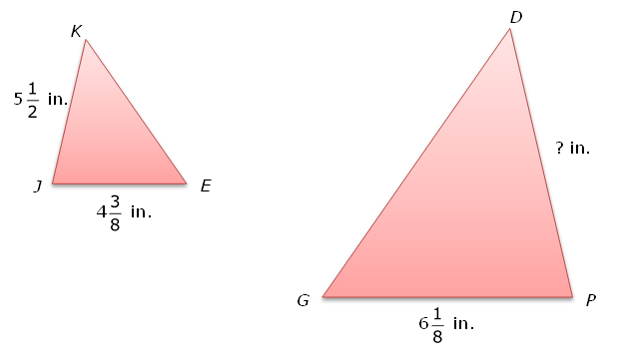
2. Triangle JKE is similar to triangle PDG. What is the length of PD?
Using Proportions with Similar Figures
Marcellus is a photographer, and he wants to enlarge the picture below into a poster with a width of 24 inches. The original dimensions of the picture are a width of 11 inches and a height of 14 inches. What will be the height of the poster?

Now that you have correctly identified the proportion, solve for x and calculate the height of the poster. Round your answer to the nearest 0.1.
Practice
1. To estimate the height of a pagoda, Shoji placed a mirror along the ground 15.7 meters from the base of the pagoda.
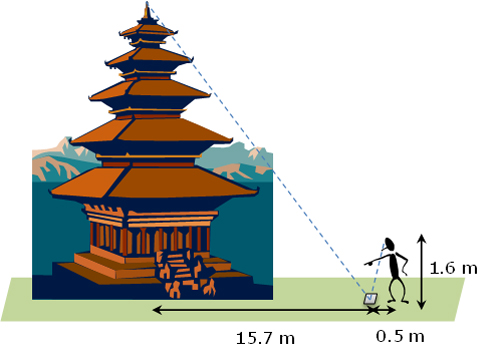
Shoji is 1.6 meters tall, and stood 0.5 meters from the mirror. To the nearest meter, about how tall is the pagoda?
2. A pyramid that is used for the 8th grade dance is 10 feet tall and has a base length of feet. Tabletop decorations will be created that are similar to the large pyramid and have a base length of 9 inches.
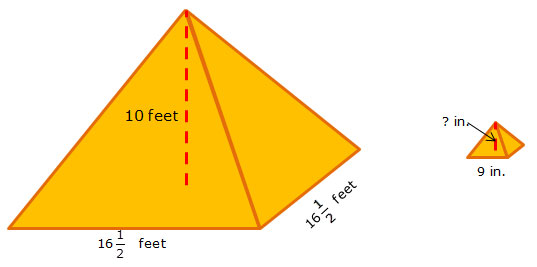
What is the height of the tabletop decorations?
