Let's Get Started
Let's learn how to write equations to describe functional relationships.
TEKS Standards and Student Expectations
A(2) Linear functions, equations, and inequalities. The student applies the mathematical process standards when using properties of linear functions to write and represent in multiple ways, with and without technology, linear equations, inequalities, and systems of equations. The student is expected to:
A(2)(C) write linear equations in two variables given a table of values, a graph, and a verbal description
Resource Objective(s)
Given a problem situation in verbal form, students will write an equation that can be used to represent the situation.
Essential Questions
What kinds of strategies can be used to identify the starting point and rate of change when given a problem situation?
When should slope-intercept form be used to write an equation for a problem situation?
When should standard form be used to write an equation for a problem situation?
Vocabulary
- Equation
- Variable
- Constant
- Linear Function
- Slope-Intercept Form
- Coefficient
- Addend
- Standard Form
Introduction
You may often encounter math problems involving money. Financial problems that you can solve using algebra include the following:
- Saving monthly
- Paying off a balance
- Determining the cost of a set of items
- Determining the amount of earnings
- Determining the amount of income taxes owed
- Determining the amount of sales taxes
- Determining earnings involving commission
Other types of problems where you may want to use algebra involve rates and accumulation of items such as the following:
- Car mileage
- Distance traveled
- Combined weight or mass of objects
Before you can use algebra to solve these types of problems, and many more, you need to know how to write equations for a problem situation. In this lesson, you will investigate different ways that you can write those equations.
Identifying Operations from Problem Situations
Before analyzing problem situations in order to write equations, let’s pause to review what different mathematical operations look like in these situations.
Remember that in order to solve a problem, you need to identify which operations to perform on rational numbers or real numbers. In Algebra, the ideas are similar, except you may now need to use those operations to work with variables, constants, or both.
Interpreting Rates of Change in Problem Situations
In other words, the quotient of a change in the y-value divided by the change in the associated x-values remains the same for any set of y-values and associated x-values.
One way that you can represent a linear function is called slope-intercept form.
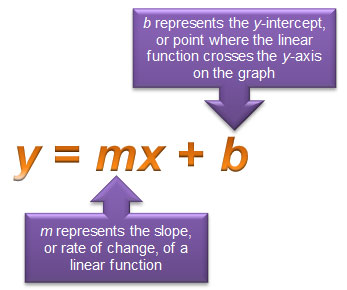
When you have a situation with a starting point, or initial condition, and a constant rate of change, you can frequently represent that situation using a linear function in slope-intercept form.
You may also see situations that result in equations written in standard form. Standard form of a linear equation is Ax + By = C. In this representation, A, B, and C are constants that show the relationship between two variables, x and y.
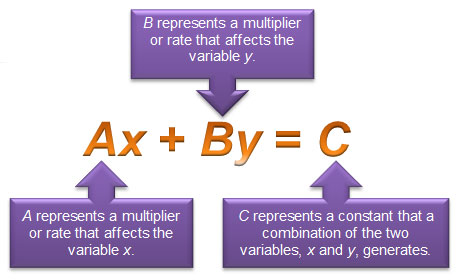
Creating Problem Situations from Equations
We've examined ways that you can write equations to describe a given situation. You can also apply that skill to do the opposite—write a situation to match a given equation.
Consider the following equation:
y = 2.50x + 18
This equation could describe any of the following situations.
| Mrs. Carmona has $18 in her cash register in the lunch line. Each lunch costs $2.50. After x more students have purchased lunches, there is a total of y dollars in Mrs. Carmona’s cash register. | Manuel’s scouting troop has $18 in their activity account. They sell raffle tickets for $2.50 each. After selling x number of tickets, there will be a total of y dollars in the activity account. | A plant is 18 inches tall. Each week, it grows an additional 2.5 inches. After x weeks, the plant will be y inches tall. |
Summary
There are many strategies for solving problems. Some of those problem-solving strategies are shown in the figure to your right.
Notice that one of those problem-solving strategies is to write and solve an equation.
Before you can use an equation to solve a meaningful real-world problem, you need to be able to write equations from the real-world problems that you encounter.
In this lesson, you have examined different ways that you can translate the problem into an algebraic equation.
- What action does the problem require? This will help me to decide which operations to include in my equation.
- Is there a starting point and a rate of change? If so, I may be able to use a linear function written in slope-intercept form.
- Does the problem involve combinations of two items that each contain a separate rate? If so, I may be able to use a linear equation written in standard form.
