Introduction
In the past, you may have written and solved equations with variables on both sides of the equation. Some situations in Geometry lend themselves to writing and solving equations. In this lesson, you will use informal arguments to establish some geometric facts. Then, you will use those facts to set up and solve equations.
A pipeline that crosses two parallel roads creates special angle relationships.
Street patterns, such as this one in Jerusalem, create triangles that also have special angle relationships.

Source: Jerusalem triangle.jpg, Orrling, Wikimedia Commons
There are also special relationships found in similar triangles.

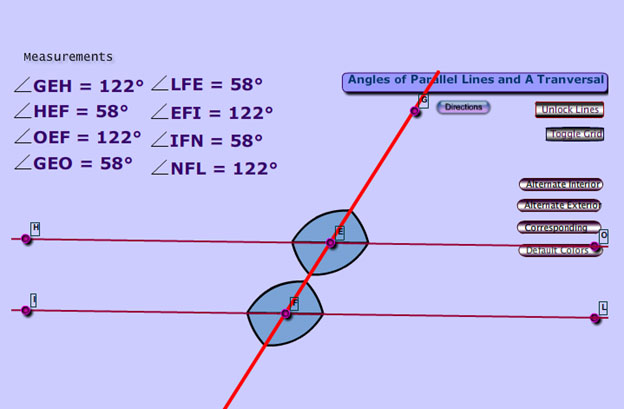
Using Informal Arguments with Parallel Lines
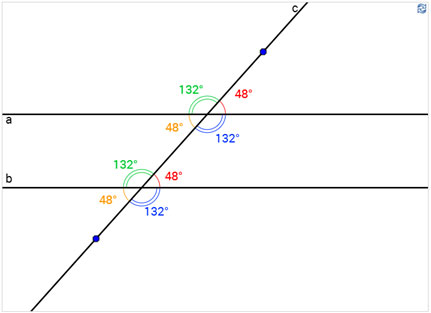
In this section, you will investigate relationships among angle pairs created by two parallel lines that are crossed by a transversal.
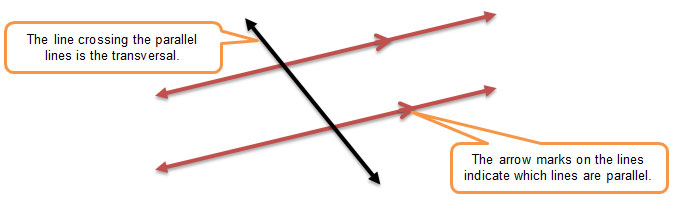
Use the interactive below to investigate the five relationships of angles formed by parallel lines and a transversal. Click the image to open the interactive, and it will open in a new browser tab or window. Drag the blue points to change the transversal. As you do so, notice how the angle measured for the eight labeled angles changes.
Use the interactive to answer the questions below.
1. Corresponding angles are angles that are at the same location at each intersection. In the interactive, they are color-coded to match. What do you notice about the measures of corresponding angles?
2. Alternate interior angles are angles that are on opposite sides of the transversal and between the two parallel lines. What do you notice about the measures of alternate interior angles?
3. Alternate exterior angles are angles that are on opposite sides of the transversal and outside the two parallel lines. What do you notice about the measures of alternate exterior angles?
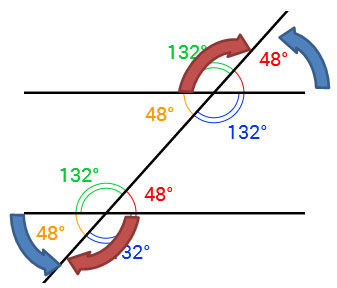
4. Consecutive interior angles are angles that are on the same side of the transversal and between the parallel lines. What do you notice about the measures of consecutive interior angles?
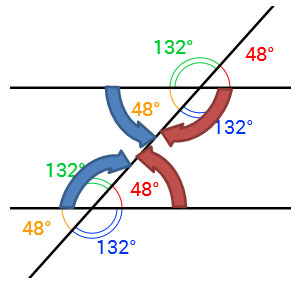
5. Consecutive exterior angles are angles that are on the same side of the transversal and outside the two parallel lines. What do you notice about the measures of consecutive exterior angles?
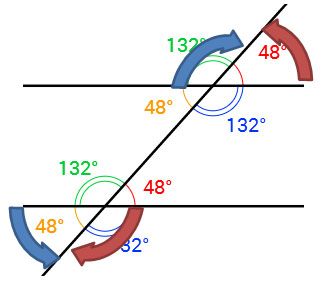
Pause and Reflect
1. What patterns do you see in angle pairs that are congruent?
2. What patterns do you see in angle pairs that are supplementary?
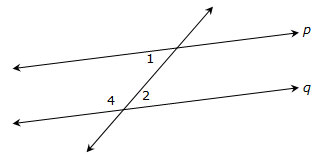
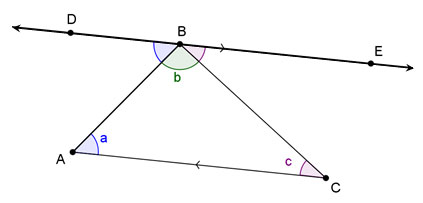
1. In the diagram below, p ∥ q. ∠1 and ∠2 are alternate interior angles. ∠1 and ∠4 are consecutive interior angles. Using these facts explain why ∠1 and ∠4 must be supplementary.
In the diagram below, transversal l crosses parallel lines b and c. Use this diagram to answer questions 2 and 3.
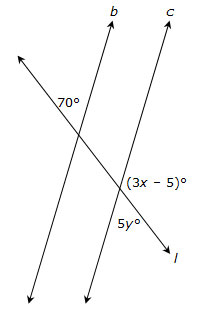
2. Write an equation that you can use to solve for x. Which relationship did you use?
3. Write an equation that you can use to solve for y. Which relationship did you use?
4. Determine the value of x and y.
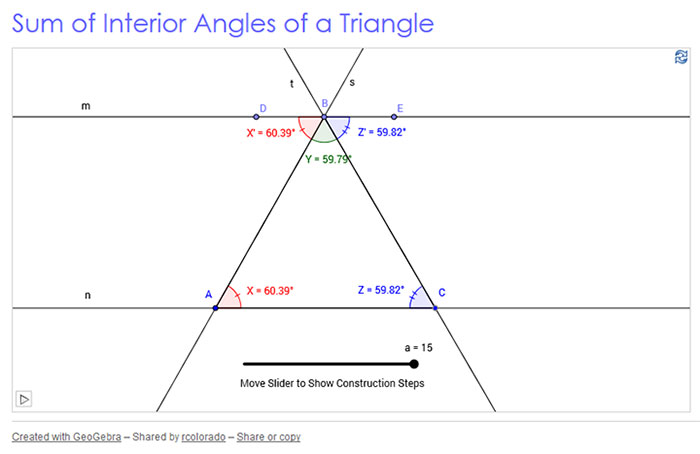
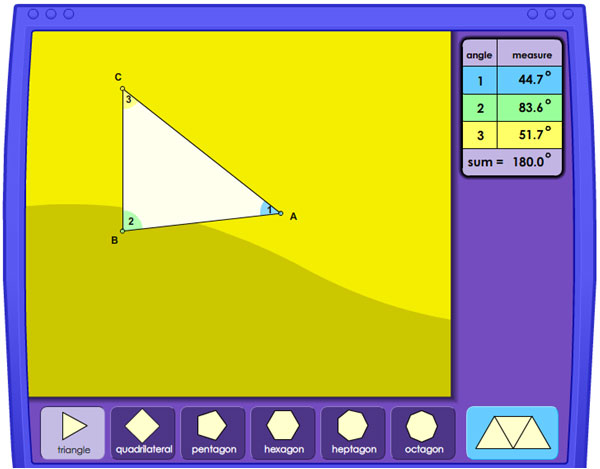
Using Informal Arguments with Triangle Angle Relationships
In the last section, you investigated relationships between pairs of angles created when a transversal crosses two parallel lines. In this section, you will investigate and use informal arguments to describe two important relationships among the angles of a triangle:
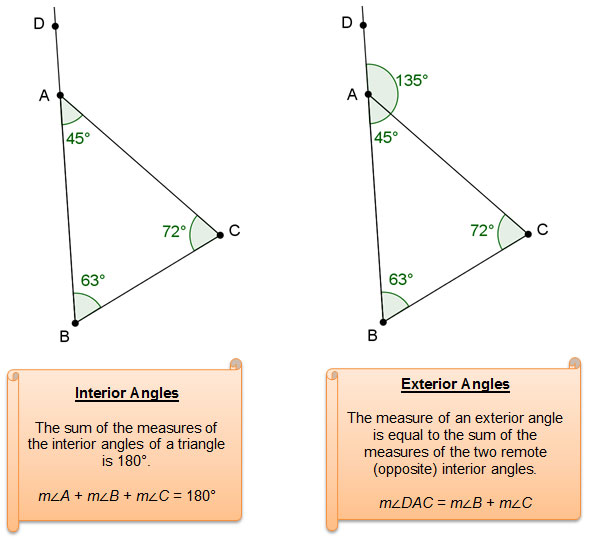
- the sum of the measures of the interior angles and
- the measure of an exterior angle as compared to certain interior angles.
Click on the image below to access the interactive. Use the interactive to investigate the relationship among the measures of the three interior angles of a triangle. Click on the arrow in the bottom left corner or slowly drag the slider at the bottom. Notice the congruent angles.
Use the interactive to answer the questions below.
1. In the interactive, line m ∥ line n, how is ∠BCA(∠Z) related to ∠CBE(∠Z)?
2. In the interactive, line m ∥ line n, how is ∠BAC(∠X) related to ∠DBA(∠X)?
3. Examine the three angles with a common vertex at point B. What is special about these three angles? What does that tell you about the angle measures?
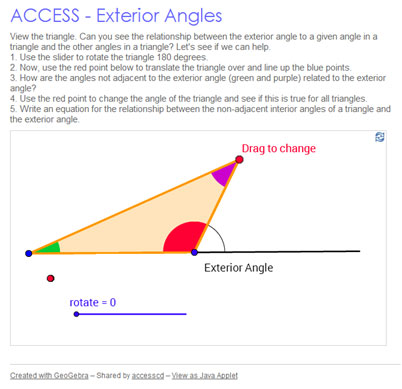
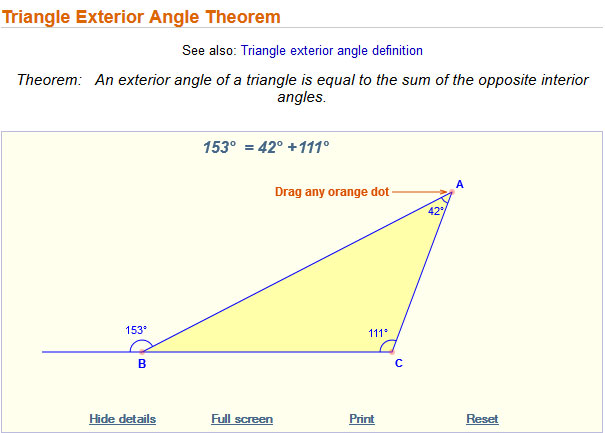
Exterior Angles of a Triangle
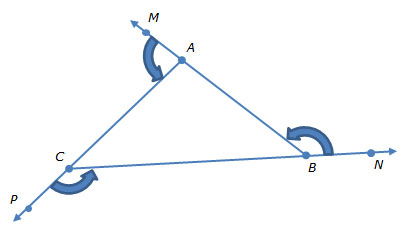
A triangle has several exterior angles, or angles formed outside the triangle by extending one of the three sides. There can be up to six exterior angles depending on which sides are extended.
In the diagram shown, triangle ABC has three exterior angles: ∠MAC, ∠ABN, and ∠PCB.
Click on the image below to access the interactive. Use the interactive below to investigate the relationship between an exterior angle of a triangle and the two opposite, or remote, interior angles. Click and drag the red vertex of the triangle to change the shape of the triangle. Use the sliders to move the interior angles to the same vertex as the exterior angle so that you can compare the measures of the three angles.
Use the interactive to answer the questions below.
1. How do the purple and green interior angles compare to the exterior angle?
2. How does the sum of the measures of the two interior angles (purple and green) compare to the measure of the exterior angle?
3. If the measure of the purple interior angle is 75° and the measure of the green interior angle is 20°, what is the measure of the exterior angle? How do you know?
Pause and Reflect
For both the sum of the interior angles of a triangle and the measure of an exterior angle of a triangle, straight lines were important. Thinking about the number of degrees there are in an angle created by one straight line, why do you think that is the case?
Practice

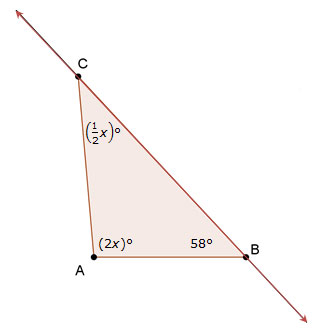
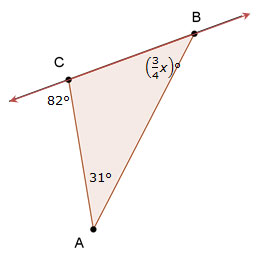
2. Write an equation that you can use to solve for x, then determine the value of x.
3. Write an equation that you can use to solve for x, then determine the value of x.
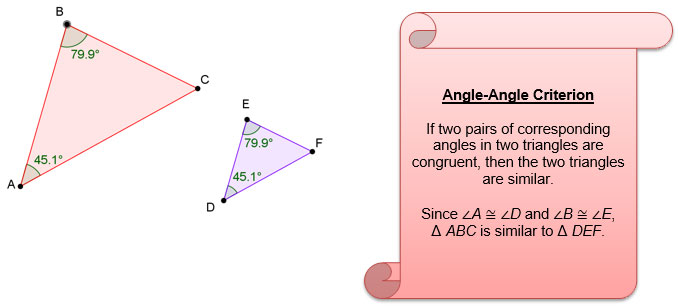
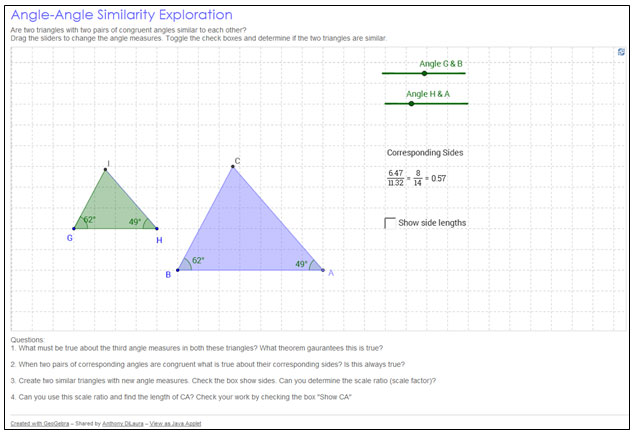
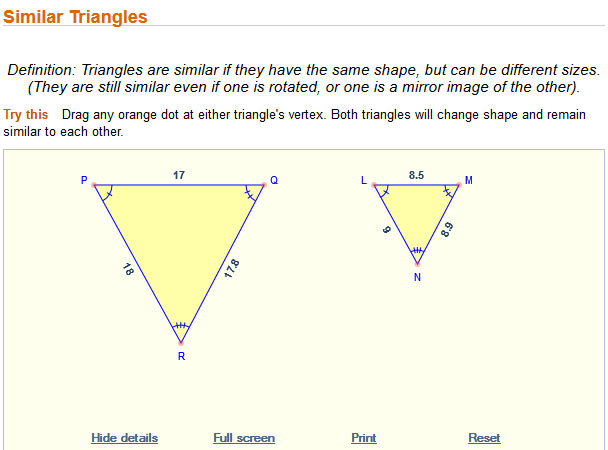
Using Informal Arguments with Similar Triangles
In previous grades, you learned that two figures are similar if all of the corresponding angles are congruent and all of the corresponding side lengths are proportional.
In this section, you will refine what you know about similar triangles in order to make arguments and solve problems about similar triangles when you only know the measures of two pairs of corresponding angles. This condition of similar triangles is called the angle-angle criterion.
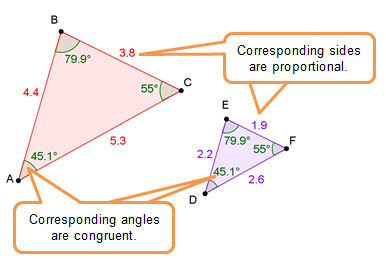
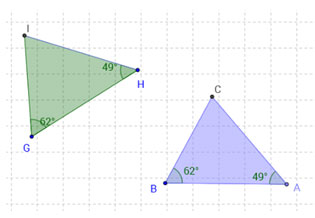
Click on the image below to access the interactive. Use the interactive to investigate two triangles, Δ ABC and Δ HGI. Use the sliders to adjust the angle values. Click and drag on points A and B to adjust the size of Δ ABC, and click and drag on points G and I to adjust the size of Δ HGI.
Use the interactive to answer the questions below.
1. If you know the measures of two interior angles in a triangle, how can you calculate the measure of the third angle?
2. Suppose that in two triangles, the measures of two pairs of corresponding interior angles are equal. What does this tell you about the measures of the third interior angle in each triangle? Explain your reasoning.
3. In the interactive, check the box to show side lengths. What do you notice about the lengths of the corresponding sides of Δ ABC and Δ HGI ?
4. Are triangles ABC and HGI similar? Explain how you know.
Pause and Reflect
For the angle-angle criterion for similarity, you know that two pairs of corresponding angles are congruent. Why do we not need to state that the third pair of corresponding angles is also congruent?
1. In the diagram below, line AB ∥ line DC, line AD, and line BC are transversals that intersect at point E. Use angle relationships between parallel lines to explain how you know that triangle ABE is similar to triangle DCE.
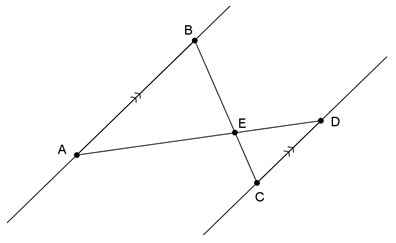
Use the diagram below to answer questions 2–4. Assume that line BC || line DE.
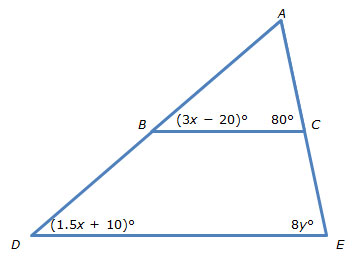
2. Write two equations that you can use to solve for x and y given that Δ ABC is similar to Δ ADE.
3. Determine the values of x and y.
4. Determine the measure of ∠ABC.
Summary
In this lesson, you investigated and then used informal arguments to show angle relationships among parallel lines with a transversal, interior, and exterior angle relationships with a triangle, and the angle-angle criterion for similar triangles.
You also used these relationships to write and solve equations.
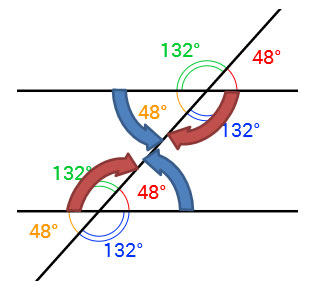
Angle Relationships in Parallel Lines
Interactive exercise. Assistance may be required. Review angle relationships by identifying the alternate interior, alternate exterior, and corresponding angles. Click on the image to access the interactive.
After observing all the angles, answer the following:
1. List all the alternate interior angles.
2. List all the alternate exterior angles.
3. List all the corresponding angles.
4. Consecutive interior angles are?
5. Consecutive exterior angles are?
Below is a diagram reviewing the above information.
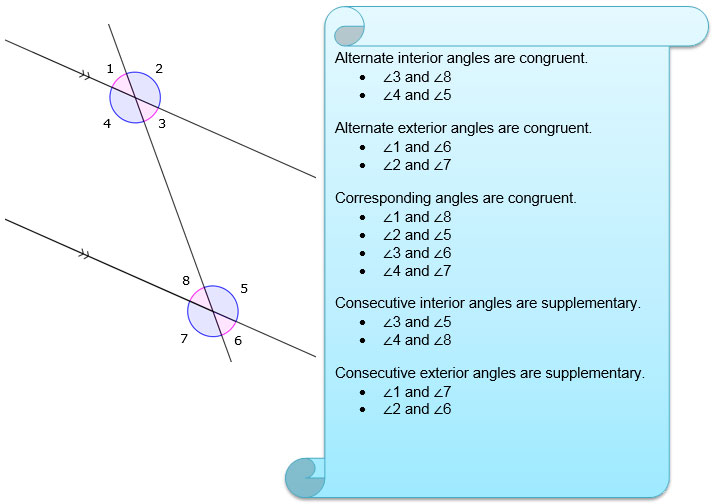
Below is a diagram reviewing the above information.
Angle-Angle Criterion for Similar Triangles
Click on the image to access the interactive. Move the points around while observing the angles and ask yourself: do any of the interior angle measures change?
NOTE: Angles with the same measures are marked with the same marks.
1. Angles R and N are congruent and corresponding angles. At any time, were the measures of these two angles not equal? Angles Q and M are congruent and corresponding angles. At any time, were the measures of these two angles not equal?
2. If two pairs of corresponding angles in two triangles are congruent, then what are the two triangles called?
Below is a diagram reviewing the above information.