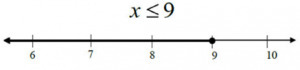Let's Get Started
We're going to learn how to graphically find the solution to one-variable and two-variable inequalities. You will also review how to convert a linear equation from standard form to slope-intercept form.
TEKS Standards and Student Expectations
A(3) Linear functions, equations, and inequalities. The student applies the mathematical process standards when using graphs of linear functions, key features, and related transformations to represent in multiple ways and solve, with and without technology, equations, inequalities, and systems of equations. The student is expected to:
A(3)(D) graph the solution set of linear inequalities in two variables on the coordinate plane
Resource Objective(s)
The student will construct the graph of a one-variable or two-variable inequality and find its solution.
The student will also convert between standard form and slope-intercept form of a linear equation.
Essential Questions
If your inequality symbol is "less than" or "greater than," what type of boundary line should you graph?
If your inequality symbol is "less than or equal to" or "greater than or equal to," what type of boundary line should you graph?
If your inequality symbol is "less than" or "less than or equal to," where is your solution region?
If your inequality symbol is "greater than" or "greater than or equal to," where is your solution region?
How do you convert an equation from standard form to slope-intercept form?
Vocabulary
- Inequality
- Boundary Line
- Dashed/Dotted
- Solid
- Standard Form
- Slope-Intercept Form
Graphing Inequalities in One Variable
For inequalities in one variable, such as x ≤ 9, solutions are graphed on a number line.
For the inequality, x ≤ 9, the solutions are graphed by drawing a closed circle at 9 and shading to the left on the number line. This indicates that all real numbers less than or equal to 9 are solutions to the inequality.
To check the shading, select a test point in the shaded area on the number line and plug it into the inequality. If the statement is true, then the shading is correct.
x ≤ 9
Test Point: 7
7 ≤ 9
True!
For the inequality x > -4, the solutions are graphed by drawing an open circle at -4 and shading to the right on the number line. This indicates that all real numbers greater than -4 are solutions to the inequality.
Here are some examples of inequalities in one variable:
Graphing Linear Inequalities in Two Variables
For inequalities in two variables, such as y ≤ 2x + 5, solutions are graphed on a coordinate plane.
For the inequality y ≤ 2x + 5, the solutions are graphed by drawing a solid line (y-intercept at 5 and slope of 2). A solid line is drawn for both ≤ and ≥.
The line represents the boundary for all solutions to the inequality. To determine on which side of the line the solutions lie, select a test point.
The test point should not lie on the line. The point (0, 0) can be chosen for this example.
Plug x = 0 and y = 0 into the inequality and simplify. If the statement is true, the point (0, 0) as well as all the other points on that side of the line are solutions to the inequality. If the statement is false, the point (0, 0) as well as all the other points on that side of the line are not solutions.
y ≤ 2x + 5
0 ≤ 2(0) + 5
0 ≤ 0 + 5
0 ≤ 5
True!
Since (0, 0) is a solution to the inequality, shade on the side of the line where (0, 0) is (below the line). This means that all real numbers on the line and in the shaded region are solutions to the inequality.
For the inequality y 1/4x – 3, the solutions are graphed by drawing a dashed/dotted line at y = 1/4x - 3 (y-intercept at -3 and slope of 1/4). A dashed/dotted line is drawn for both and >.
Using a test point of (0, 0), it can be determined that (0, 0), and all of the other points on that side of the line are solutions to the inequality.
Therefore, we shade above the line. This indicates that all real numbers in the shaded area but not on the line are solutions to the inequality
y > 1/4x - 3
0 > 1/4(0) - 3
0 > 0 - 3
0 > -3
True!
Where is the solution region?
When your inequality symbol is "greater than" (>) or "greater than or equal to" (≥), the solution region is above the boundary line. When your inequality symbol is "less than" () or "less than or equal to" (≤), your solution region is below the boundary line.
Copy the box below into your notes for reference.
| Solid Line | Dashed/Dotted Line | |
| Shade Above | ≥ | > |
| Shade Below | ≤ |
Converting Inequalities from Standard Form to Slope-Intercept Form
To graph linear inequalities given in standard form, convert to slope-intercept form and then determine the y-intercept and the slope.
Example 1
Graph 4x + 5y ≥ 15.
To convert this example to slope-intercept form, first subtract 4x from both sides of the inequality.
Then, divide all terms by 5.
4x + 5y ≥ 15
- 4x - 4x
5y ≥ -4x + 15
5 5 5
y ≥ –4/5x + 3
y-intercept: 3
slope: –4/5
In slope-intercept form, the inequality is:
y ≥ –4/5x + 3
Since the inequality symbol is ≥, draw a solid line and shade above the line.
Refer to the following table that you copied into your notes.
| Solid Line | Dashed Line | |
| Shade Above | ≥ | > |
| Shade Below | ≤ |
Example 2
Graph x – 3y > 9.
To convert this example to slope-intercept form, subtract x from both sides of the inequality and divide all terms by -3. When an inequality is divided by a negative, the symbol changes between and > or ≤ and ≥. In this case, the symbol changes from > to .
x – 3y > 9
-x -x
-3y > -x + 9
-3 -3 -3
y 1/3x – 3
y-intercept: -3
slope: 1/3
In slope-intercept form, the inequality is:
y 1/3x – 3
Since the inequality symbol is , draw a dashed line and shade below the line.
Interactive Linear Inequality
Click on this link for an interactive way to graph an equation of a linear inequality: Linear Inequality Activity.
Adjust the graph by clicking and dragging point A or point C, and the inequality will adjust accordingly. To change the sign, click on the inequality itself.
Adjust the graph on the website to correspond with the following inequalities. Then sketch the corresponding graphs on scratch paper. In your notes, write each inequality and record a description of the graphs.
- y < 0.2x + 5
- y < -2x
- y ≥ x + 1
- y > 0.5x – 3
- y ≤ x – 6
- 4x + y > 5
- 2x – 6y < 8
- x + 5y ≤ 10
Self-Assessment: Graphing Inequalities
Click on this link: Graphing Inequalities Quiz
- Answer question 1 (multiple choice).
- For question 2, describe the graph in the box provided. Possible descriptions include: solid/dashed line, y-intercept, slope, shading above/below, and any solutions to the inequality.
- Click Check Your Work.