Introduction
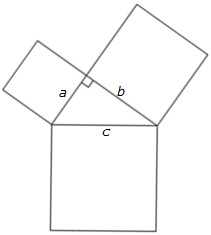
Recall the Pythagorean Theorem, or the special relationship between the lengths of the sides of a right triangle using the following formula:
a2 + b2 = c2

Source: José de Ribera, Pitágoras, Wikimedia Commons
Because so much of our world is based on rectangles and right triangles, the Pythagorean Theorem is a very special and important relationship in geometry. There are many relevant applications that require the use of the Pythagorean Theorem.

Engineers and astronomers use the Pythagorean Theorem to calculate the paths of spacecraft, including rockets and satellites.

Architects use the Pythagorean Theorem to calculate the heights of buildings and the lengths of walls.

Athletes even use the Pythagorean Theorem when they are calculating distances, which are important in determining how fast they can run or where a ball needs to be thrown.
In this lesson, you will practice using the Pythagorean Theorem to solve a variety of application problems. In doing so, you will work with irrational numbers and may need to approximate the value of an irrational number.
Calculating Distances
Frequently, the Pythagorean Theorem is used to calculate distances that are not easy to measure directly.

The Ladder Problem
In the diagram, a ladder that is 40 feet in length is placed against a building. The bottom of the ladder touches the ground 8 feet from the base of the building. How high above the ground will the ladder touch the building?
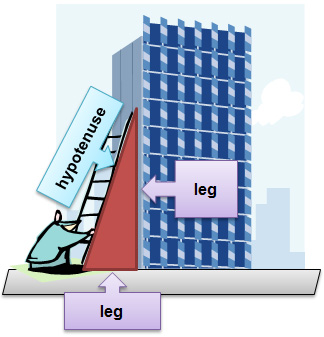
First, identify the right triangle in the diagram. In addition, identify the legs and hypotenuse of the right triangle.
Drag the appropriate measurements to the parts of the figure in order to label the diagram.
Use the Pythagorean Theorem to set up an equation for x.
Now that you have correctly set up your equation, solve for x. Express your answer as an irrational number, and then approximate to the nearest whole number.
Working with Perimeter
Another important application of the Pythagorean Theorem involves determining the perimeter of polygons.
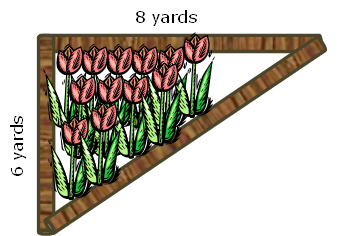
The Flowerbed Problem
Rosemary wants to plant a tulip garden in her backyard. She needs to build a triangular flowerbed using landscaping timbers. How many feet of landscaping timbers does Rosemary need to purchase?
Use the Pythagorean Theorem to set up an equation for x.
Now that you have correctly set up your equation, solve for x.

You may have solved for x, but that does not mean we have answered the question yet. Remember that the problem asked us to determine the total length of landscaping timbers that Rosemary must purchase for her flowerbed.
Use the information you know to determine the total length of landscaping timbers that Rosemary must purchase in order to completely surround her flowerbed.
Additional Applications
The Pythagorean Theorem can also be used to determine lengths of segments that may be formed by multiple right triangles or other polygons. The Pythagorean Theorem will only work to show you the relationship between the side lengths of a right triangle. But once you know that information, you can use it to solve larger problems.
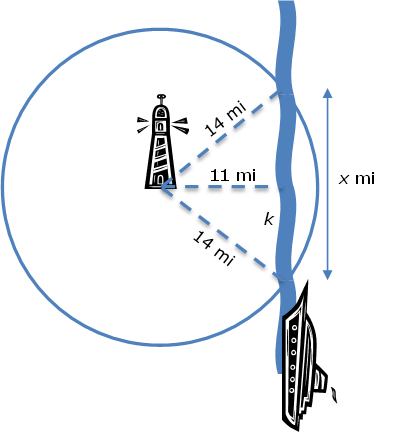
The Lighthouse Problem
A boat is sailing parallel to the shore and passes a lighthouse. The beam from the lighthouse is visible for 14 miles. The boat passes the lighthouse along the path shown in the diagram and at its closest point is 11 miles from the lighthouse. For how many miles will the captain of the boat be able to see the lighthouse?
Use the Pythagorean Theorem to set up an equation for k.
Now that you have correctly set up your equation, solve for k. Express your answer both as an irrational number and approximated to the nearest tenth of a mile.
Now that we know the value of k, we can use that to answer the original question. For how many miles will the captain of the boat be able to see the lighthouse?
The Pillow Problem
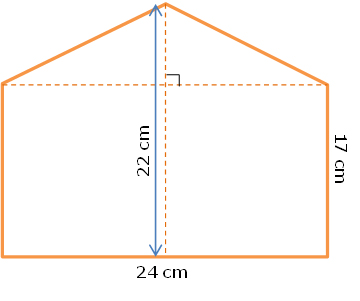
A large pillow is in the shape of a pentagon as shown. Meredith wants to sew a cord around the edge of the pillow for a decoration. What is the length of the cord that Meredith needs in order to completely cover the edge of the pillow?
 Strategy: First, we need to look for right triangles in the picture. Once we have identified the right triangles, we need to determine the dimensions of the right triangles.
Strategy: First, we need to look for right triangles in the picture. Once we have identified the right triangles, we need to determine the dimensions of the right triangles.Use the figure, along with the Pythagorean Theorem, to calculate the length of each side of the pillow. Click on the plus signs on the image to check your answers.
Determine the total length of cord that Meredith should use.