Introduction
In previous grades, you learned that the volume of an object is the number of cubic units in the interior of a three-dimensional figure.
 For the rectangular prism shown, there are five layers of 12 cubes each. This prism has a width of 4 units, length of 3 units, and height of 5 units. Counting the cubes reveals that the rectangular prism has a volume of 60 cubic units.
For the rectangular prism shown, there are five layers of 12 cubes each. This prism has a width of 4 units, length of 3 units, and height of 5 units. Counting the cubes reveals that the rectangular prism has a volume of 60 cubic units.
In this lesson, you will investigate other ways to calculate the volume of rectangular prisms and triangular prisms. You will use volume formulas to solve problems involving volume of prisms.
To begin this lesson, watch the video below that compares the area of a two-dimensional figure with the volume of a related three-dimensional figure. The video also compares the volume of triangular prisms to the volume of rectangular prisms.
Based on what you saw in the video, answer the following questions:
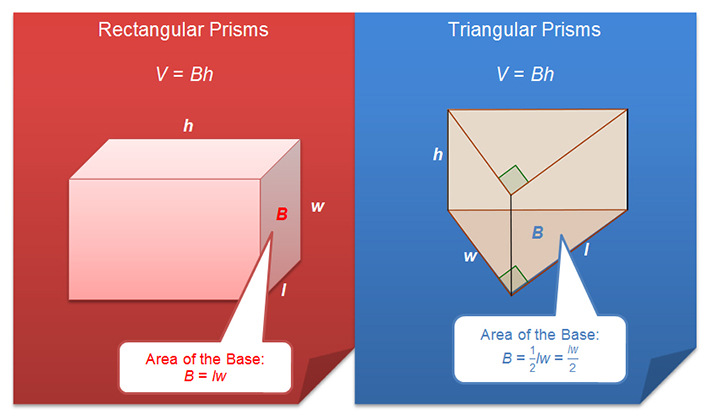
Solving Problems Involving the Volume of Rectangular Prisms
In the introduction, you reviewed some area formulas that you can use to calculate the area of rectangles or triangles. You also reviewed the volume formula for rectangular prisms.
In this section, you will investigate the volume formula for a rectangular prism more fully, and use the volume formula to solve problems.
Use the interactive below to explore the volume formula for rectangular prisms. Use what you see to answer the questions that follow.
|
Pause and Reflect 1. The number of cubes in the bottom layer is the area of the base of the prism, B. The number of layers is the height of the prism, h. Write a formula that relates the volume of the prism, V, to the area of the base of the prism, B, and the height of the prism, h. 2. A rectangular prism has a base with dimensions 6 centimeters by 8 centimeters and a height of 4 centimeters. What is the volume of the prism? |
Solving Problems Involving the Volume of Triangular Prisms
 In the last section, you developed the volume formula for a prism, V = Bh, where B represents the area of the base of the prism, and h represents the height of the prism. You also used the volume formula to solve problems involving rectangular prisms.
In the last section, you developed the volume formula for a prism, V = Bh, where B represents the area of the base of the prism, and h represents the height of the prism. You also used the volume formula to solve problems involving rectangular prisms.
However, not all prisms are rectangular prisms. Consider the skyscrapers from different cities that are shown below.
|
The Flatiron Building in New York City is a triangular prism since the roof and street outline are congruent right triangles. |
The JPMorgan Chase Tower in Houston is a pentagonal prism since the roof and street outline are congruent pentagons. |
The Tower in Fort Worth is an octagonal prism since the roof and street outline are congruent octagons. |

Source: Edificio Fuller (Flatiron) Edit, lmelenchon, Wikimedia Commons |
 |

Source: The Tower, 500 Throckmorton, Fort Worth, Texas, Magnus Manske, Wikimedia Commons |
In this section, you will focus on triangular prisms, which are prisms with triangular bases.
Use the interactive to create several triangular prisms. Use the dimensions in the interactive to make the calculations to complete the table below. Record the volume of the prism from the interactive. Use the table to answer the questions that follow.
Copy the table below into your notes or a word processing document to enter the data into the table.
| Prism Number | Area of Base | Height of Prism | Volume of Prism |
|
1
|
6.18
|
5
|
30.9
|
|
2
|
|||
|
3
|
|||
|
4
|
Questions
1. How did you calculate the area of the base of the triangular prism?
2. When calculating the area of the triangle, how did you know which two dimensions to use?
3. In the table, how does the product of the area of the base and the height of the prism compare to the volume of the prism from the interactive?
4. Write a volume formula that can be used to calculate the volume of a triangular prism. Use B for the area of the base and h for the height of the prism.
|
Pause and Reflect 1. How is calculating the volume of a triangular prism like calculating the volume of a rectangular prism? 2. How is calculating the volume of a triangular prism different from calculating the volume of a rectangular prism? |
Practice
For questions 1–3, each composite figure is broken into different component regions. Identify the area formula required to calculate the area of each component region.
Summary
In this lesson, you learned how to apply volume formulas for prisms in order to solve problems involving rectangular prisms and triangular prisms. As you noticed, there are also many other types of prisms. However, you will learn more about determining the volumes of those prisms in later lessons.