Introduction
As you have seen in previous grades, an expression is a mathematical statement that uses numbers, variables, and operations to show a relationship between certain quantities.
These are all examples of expressions that you may have seen.
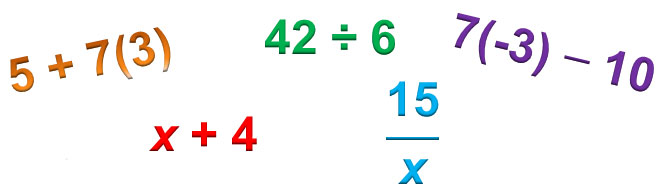
If two expressions are equal, then the resulting mathematical sentence is an equation. These are examples of equations that you may have seen.
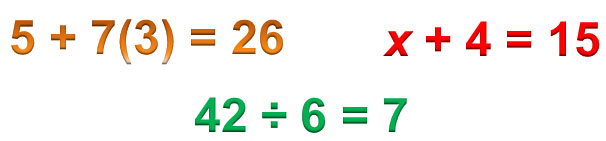
Because the two expressions on each side of the equation are equal, you will see the metaphor of a balanced scale used to represent the two sides of the equation.
For example, the equation 5 = 3 + 2 is shown in the image below using a balanced scale.
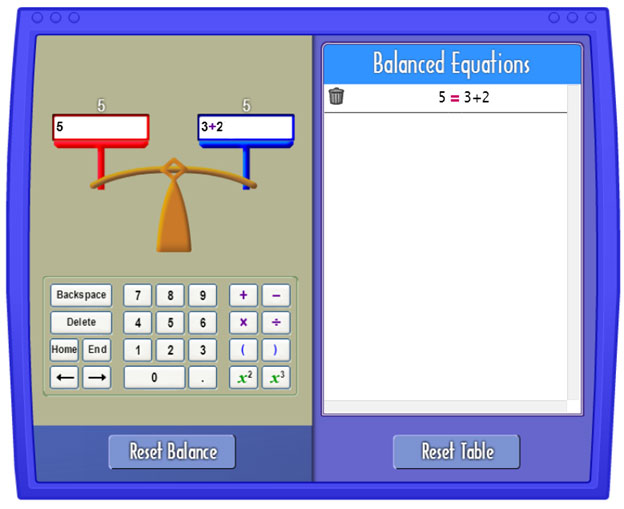
Use the interactive linked to the image below to explore the relationship between the following pairs of expressions. The interactive will open in a new browser tab or window. If the scale is balanced, then the expressions are equal, and you can write an equation to represent the relationship between the two expressions. If the scale is not balanced, then the expressions are not equal.
- 3(4) and 24 ÷ 2
- 3(8 − 3) and 13 + 2
- 27 ÷ 3 and 3 × 3
Now that you’ve investigated the idea of balance as it relates to numerical expressions, in this lesson, you will extend that idea to algebraic equations. You will use a variety of models to represent and solve algebraic equations, which involve relationships between numbers and variables.
Using Balances to Solve Equations
In the introduction, you used a balance scale to compare numerical expressions. In this section, you will use a balance scale to model and solve equations.

Consider the equation below.

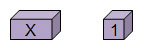
For the balance scale model, use the following figures to represent x and 1. You can represent combinations of x and 1 using combinations of the figures.
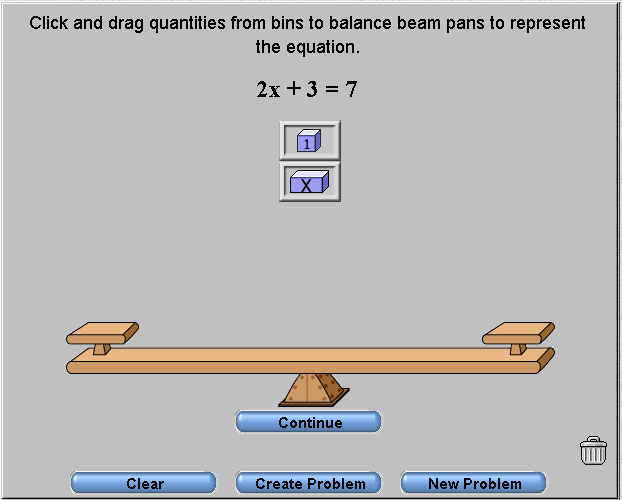
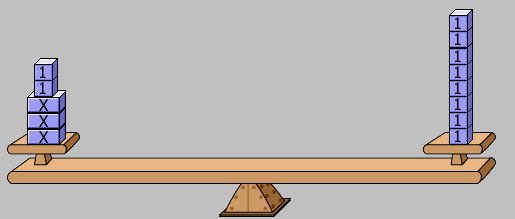
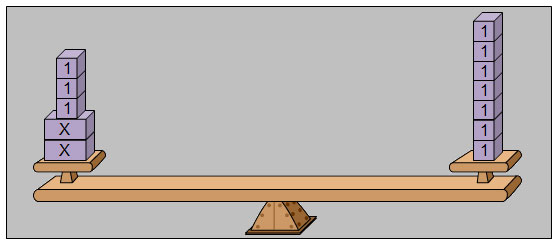
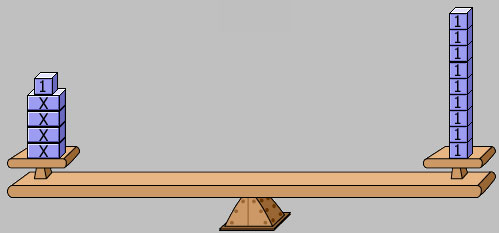
The equation, 2x + 3 = 7, can be built on the balance shown below.
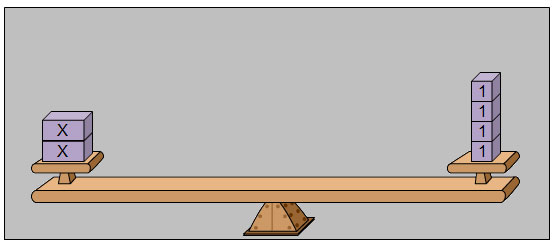
Once the equation is built on the model, the unit blocks, or 1-blocks, can be removed from both sides of the balance to determine the number of unit blocks it takes to balance the 2 x-blocks.
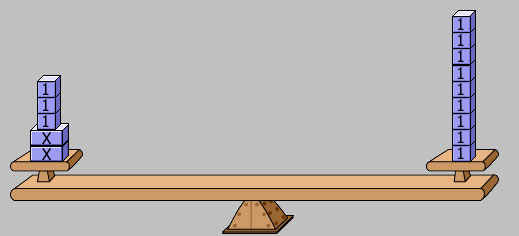
Each x-block must balance the same number of unit blocks, so in this case, each x-block balances 2 unit blocks. According to the model, x = 2.
Watch this equation being solved using the balance model.
Use the interactive below to set up at least 3 equations that will be given to you. The interactive will open in a new browser tab or window. If you need to, click New Problem until you get a two-step equation, or an equation of the form ax + b = c. Use the following steps to help you navigate through the interactive as you set up and solve the given equation.
- Use the x-blocks and unit blocks (1-blocks) to set up the equation.
- Once the equation is correctly set up, click Continue to solve the equation using the balance scale model.
- Identify the operation that needs to be performed to get the x-blocks by themselves on the balance by clicking on the symbol for that operation.
- Enter the number of blocks that need to be added, subtracted, multiplied, or divided.
- Repeat for an additional operation if you need to.
There are directions on the side panel that you can use to step through each equation. If you need additional directions, see below.
Need additional directions to set up the equation?
Need additional directions to solve the equation?
Pause and Reflect
An equation of the form ax + b = c, where a, b, and c are numbers and a is not equal to 0, is called a two-step equation.
Why do you think these equations are called two-step equations?
How would you solve an equation like 3x − 5 = 10, where b is a negative number?
2. 2x + 3 = 9
3. 4x + 1 = 9
Using Cups and Counters to Solve Equations
In the last section, you used a balance scale model to set up and solve two-step equations. In this section, you will use a different model composed of cups and counters.
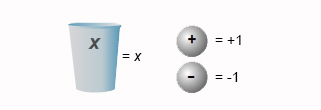
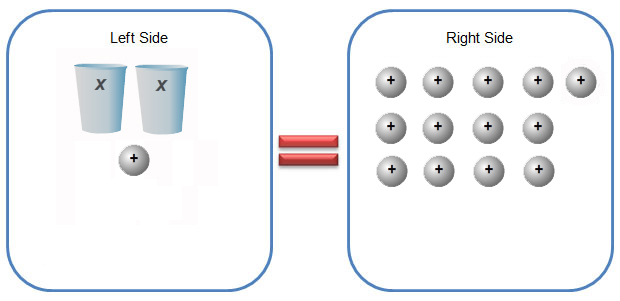
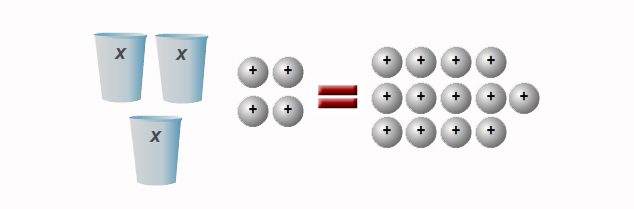
For the cups and counters model, a cup represents the variable, usually x, and counters are used to represent numbers.
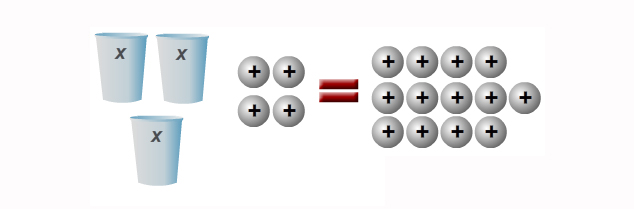
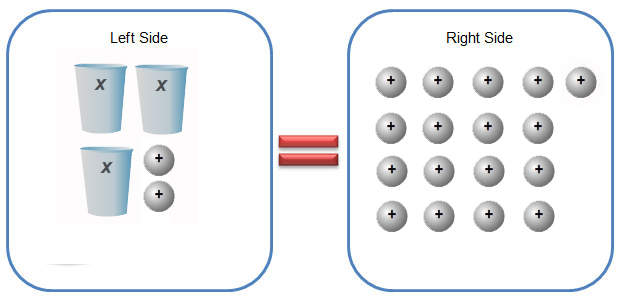
Consider the equation 3x + 4 = 13. This equation can be modeled with cups and counters with 3 cups and 4 positive unit counters on the left side of an equal sign and 13 positive counters on the right side of an equal sign.
Use the interactive below to see how Sandy used cups and counters to solve this equation.
Pause and Reflect
- When you are dividing counters evenly among the cups, what do you do if there is a counter left over?
- If you have negative counters instead of positive counters, what action do you need to take instead of removing counters from both sides of the model?
Practice
For questions 1–3, use the cups and counters model to determine the value of x.
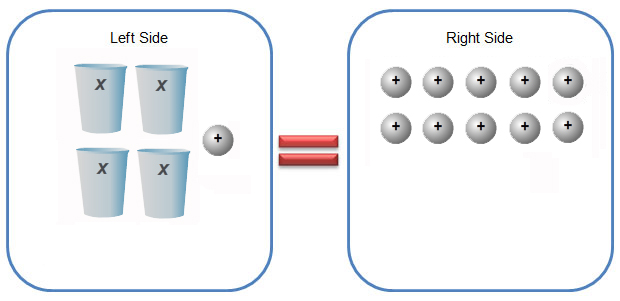
1. 3x + 2 = 17
2. 2x + 1 = 13
3. 4x + 1 = 10
Using Algebra Tiles to Solve Equations
So far in this lesson, you have seen two models for solving equations: a balance scale and cups and counters. In this section, you will use and investigate a third model, algebra tiles.
For algebra tiles, a rectangle represents the variable, usually x, and squares are used to represent numbers.
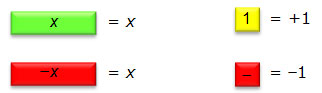
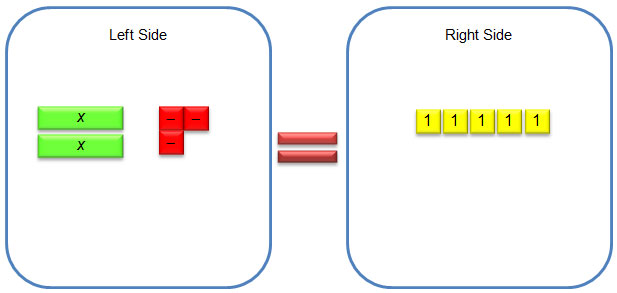
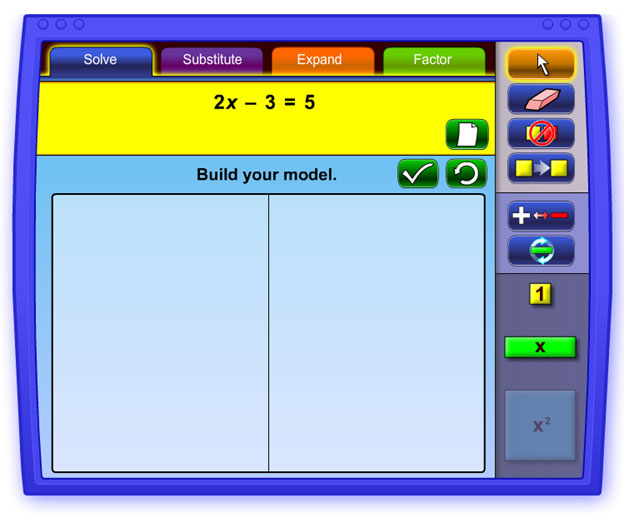
Consider the equation 2x − 3 = 5. This equation can be modeled with algebra tiles using 2 green rectangles (positive x-tiles) and 3 red squares (negative unit tiles) on the left side of the equal sign and 5 yellow squares (positive unit tiles) on the right side.
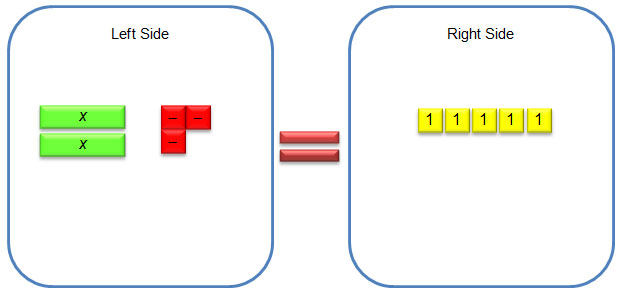
Watch this equation being solved using the algebra tile model.
On your own, use the interactive linked to the image below to set up and solve equations with algebra tiles.
- Click the "New Equation" button, the piece of paper in the yellow panel, to generate a two-step equation of the form ax + b = c.
- Use the tools to set up the equation, and click the Check tool to check your model.
- Once you have the correct setup, use zero pairs and remove tiles as necessary to solve the equation.
- Type your solution into the text box, and click the Check tool to check your answer.
Pause and Reflect
- How does the algebra tile model allow you to better visualize the concept of zero pairs?
- How does the algebra tile model compare to the cups and counter model or the balance scale model?
Practice
For questions 1–3, use the algebra tile model to determine the value of x.
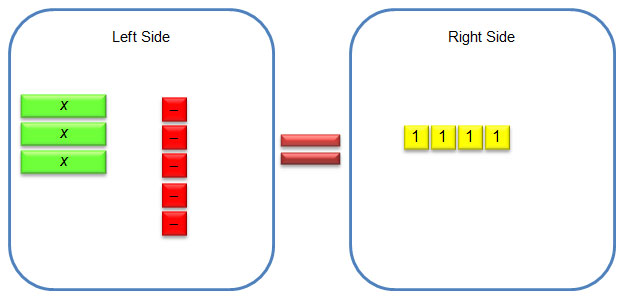
1. 4x − 5 = 15
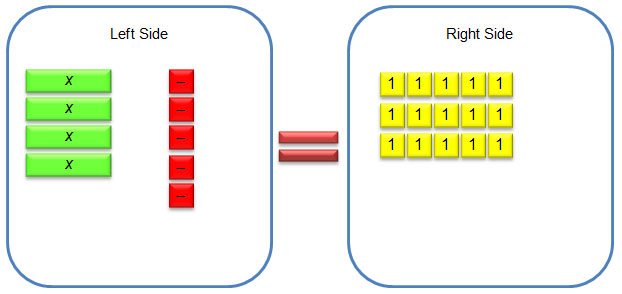
2. 2x + 7 = 3
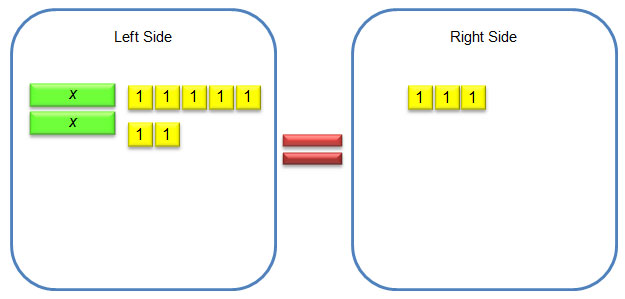
3. 3x − 5 = 4
Summary
In this lesson, you used three different models to represent and solve equations.
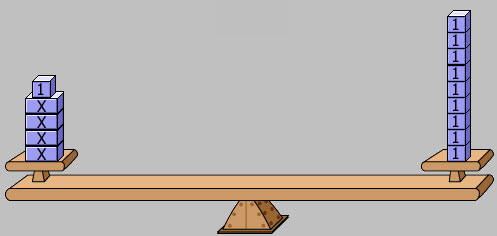
Model 1: Balance Scale
The balance scale model uses the metaphor of a balance scale in order to represent the expressions on each side of an equation. Because the expressions must have equivalent values, the scale must be balanced. Any changes made to one expression must also be made to the other in order to preserve balance.
Model 2: Cups and Counters
The cups and counters model uses cups to represent the variable and counters to represent numbers. Counters can be manipulatives such as color tiles, two-color counters, or objects such as beans. When solving equations using the cups and counters model, the goal is to determine the number of counters that go inside the cup in order to make the equation true.
Model 3: Algebra Tiles
The algebra tile model uses squares to represent numbers (units) and rectangles to represent variables (x). Green or yellow tiles are positive, and red tiles are negative. The algebra tile model allows you to visualize using zero pairs to solve equations and leads to the idea of using inverse operations to solve equations, which you will learn about in a future lesson.