Introduction
Rates and ratios can be used to solve a variety of real-world problems.
You can use rates to determine the price of a certain number of pounds of fruit.
Ratios can also help you to solve problems with percents.
You can also use ratios to solve scaling problems.

In this resource, you will extend what you know about ratios and proportions to geometry, and use ratios and proportions to describe two figures that are scaled figures.
Similar Figures
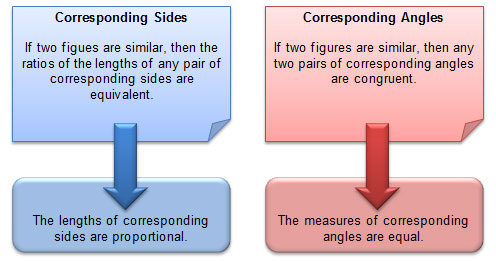
Ratios can be used to show a multiplicative relationship between two quantities. When two ratios are equivalent, you can use a proportion to relate the ratios.
Two figures are said to be similar if they are proportionally related. In this section, you will investigate the relationship between corresponding side lengths and corresponding angle measures of similar figures. From that investigation, you will make a formal definition of similar figures.
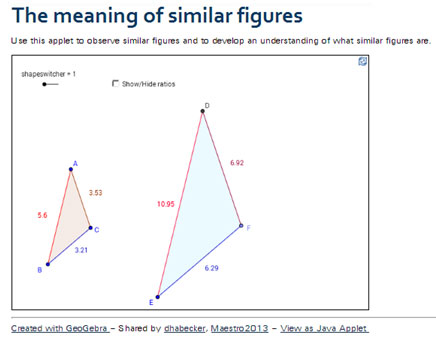
Use the interactive to begin your investigation of similar figures. In this interactive, triangle ABC and triangle DEF are similar triangles. Use the check boxes to reveal or hide ratios of the lengths of corresponding sides and to reveal or hide the measures of corresponding angles. Move the vertices of triangle ABC around, and pay special attention to patterns in the ratios of the lengths of corresponding sides and to patterns in the measures of corresponding angles.
Investigating Similar Figures
Click and drag on A, B, or C to adjust the size of triangle ABC.
Click on the Show/Hide Ratios box to show or hide the ratios of the lengths of corresponding sides.
Click on the Show/Hide Angle Measures box to show or hide the angle measures.
Use the interactive to answer the following questions.
1. Given that the two triangles are similar, what did you notice about the ratios of the lengths of the corresponding sides of triangle ABC and triangle DEF?
2. Given that the two triangles are similar, what did you notice about the measures of the corresponding angles of triangle ABC and triangle DEF?
3. Use what you noticed about the ratios of the lengths of the corresponding sides and the measures of the corresponding angles to write a definition of similar triangles.
4. Do you think the relationship you noticed for triangles would be true for quadrilaterals and other polygons?
Pause and Reflect
Now that you have a definition of similarity, how could you check to see if two figures are similar?
Identifying Corresponding Parts
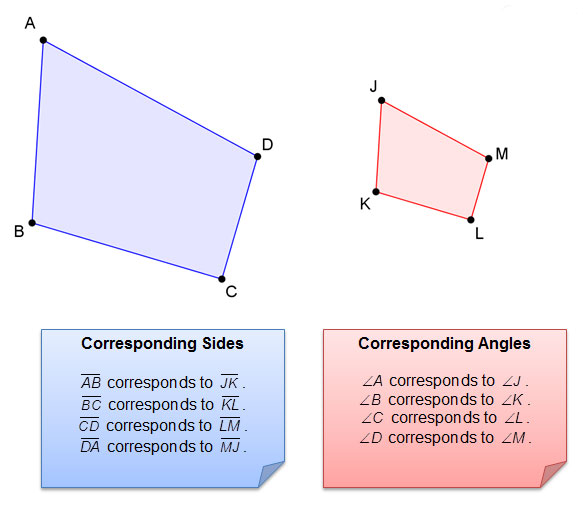
In the last section, you used characteristics of corresponding parts of similar figures in order to define similarity. If the figures are oriented the same, it is relatively easy to identify corresponding parts of similar figures.
For example, in the figure below, quadrilateral ABCD is similar to quadrilateral JKLM.
Sometimes, identifying corresponding parts is a little trickier. In this section, you will practice using different ways to identify corresponding parts of similar figures.
In the figure below, kite ABCD is similar to kite WXYZ. Match each side or angle in kite WXYZ to its corresponding part of kite ABCD by dragging the label to the appropriate blank.
Conclusion Questions
1. How can you use the angle markings to match corresponding angles?
2. How can you use known pairs of corresponding angles to determine corresponding sides?
Pause and Reflect
Why do you think it is important to be able to identify corresponding parts of similar figures?
Ratios and Proportions with Corresponding Parts
In previous sections, you have defined similarity and used similar figures to identify corresponding parts. With that experience, you are ready to use corresponding sides to solve problems!
Consider the following problem.

The slides below illustrate how Joaquin used similar triangles to write a proportion to solve this problem.
Pause and Reflect
1. What is another proportion, that Joaquin could use to solve the palm tree problems?
2. Suppose you had two similar isosceles triangles. What would you know about the base angles, the lengths of the legs of each triangle, and the ratios of the lengths of the corresponding legs?
Summary
In this resource, you learned how similar figures are defined by two main attributes.