Learning Objectives
Learning Objectives
By the end of this section, you will be able to do the following:
- Explain behaviors of waves, including reflection, refraction, diffraction, interference, and coherence, and describe applications based on these behaviors
- Perform calculations related to applications based on wave properties of light
| differential interference contrast (DIC) | diffraction grating | iridescence |
| laser | monochromator | Rayleigh criterion |
| resolution |
Wave-Based Applications of Light
Wave-Based Applications of Light
In 1917, Albert Einstein was thinking about photons and excited atoms. He considered an atom excited by a certain amount of energy and what would happen if that atom were hit by a photon with the same amount of energy. He suggested that the atom would emit a photon with that amount of energy, and it would be accompanied by the original photon. The exciting part is that you would have two photons with the same energy and they would be in phase. Those photons could go on to hit other excited atoms, and soon you would have a stream of in-phase photons. Such a light stream is said to be coherent. Some four decades later, Einstein’s idea found application in a process called, light amplification by stimulated emission of radiation. Take the first letters of all the words (except by and “of”) and write them in order. You get the word laser (see Figure 17.2 (a)), which is the name of the device that produces such a beam of light.
Laser beams are directional, very intense, and narrow (only about 0.5 mm in diameter). These properties lead to a number of applications in industry and medicine. The following are just a few examples:
- This chapter began with a picture of a compact disc (see Figure 17.1). Those audio and data-storage devices began replacing cassette tapes during the 1990s. CDs are read by interpreting variations in reflections of a laser beam from the surface.
- Some barcode scanners use a laser beam.
- Lasers are used in industry to cut steel and other metals.
- Lasers are bounced off reflectors that astronauts left on the Moon. The time it takes for the light to make the round trip can be used to make precise calculations of the Earth-Moon distance.
- Laser beams are used to produce holograms. The name hologram means entire picture (from the Greek holo-, as in holistic), because the image is three-dimensional. A viewer can move around the image and see it from different perspectives. Holograms take advantage of the wave properties of light, as opposed to traditional photography which is based on geometric optics. A holographic image is produced by constructive and destructive interference of a split laser beam.
- One of the advantages of using a laser as a surgical tool is that it is accompanied by very little bleeding.
- Laser eye surgery has improved the vision of many people, without the need for corrective lenses. A laser beam is used to change the shape of the lens of the eye, thus changing its focal length.
Virtual Physics
Lasers
This animation allows you to examine the workings of a laser. First view the picture of a real laser. Change the energy of the incoming photons, and see if you can match it to an excitation level that will produce pairs of coherent photons. Change the excitation level and try to match it to the incoming photon energy.
In the animation there is only one excited atom. Is that the case for a real laser? Explain.
- No, a laser would have two excited atoms.
- No, a laser would have several million excited atoms.
- Yes, a laser would have only one excited atom.
- No, a laser would have on the order of 1023 excited atoms.
An interesting thing happens if you pass light through a large number of evenly-spaced parallel slits. Such an arrangement of slits is called a diffraction grating. An interference pattern is created that is very similar to the one formed by double-slit diffraction (see Figure 17.8 and Figure 17.10). A diffraction grating can be manufactured by scratching glass with a sharp tool to form a number of precisely positioned parallel lines, which act like slits. Diffraction gratings work both for transmission of light, as in Figure 17.15, and for reflection of light, as on the butterfly wings or the Australian opal shown in Figure 17.16, or the CD pictured in the opening illustration of this chapter. In addition to their use as novelty items, diffraction gratings are commonly used for spectroscopic dispersion and analysis of light. What makes them particularly useful is the fact that they form a sharper pattern than do double slits. That is, their bright regions are narrower and brighter, while their dark regions are darker. Figure 17.17 shows idealized graphs demonstrating the sharper pattern. Natural diffraction gratings occur in the feathers of certain birds. Tiny, fingerlike structures in regular patterns act as reflection gratings, producing constructive interference that gives the feathers colors not solely due to their pigmentation. The effect is called iridescence.
Snap Lab
Diffraction Grating
- A CD (compact disc) or DVD
- A measuring tape
- Sunlight near a white wall
Instructions
- Hold the CD in direct sunlight near the wall, and move it around until a circular rainbow pattern appears on the wall.
- Measure the distance from the CD to the wall and the distance from the center of the circular pattern to a color in the rainbow. Use those two distances to calculate . Find .
- Look up the wavelength of the color you chose. That is .
- Solve for d.
- Compare your answer to the usual spacing between CD tracks, which is 1,600 nm (1.6 μm).
How do you know what number to use for m?
- Count the rainbow rings preceding the chosen color.
- Calculate m from the frequency of the light of the chosen color.
- Calculate m from the wavelength of the light of the chosen color.
- The value of m is fixed for every color.
Fun In Physics
CD Players
Can you see the grooves on a CD or DVD (see Figure 17.18)? You may think you can because you know they are there, but they are extremely narrow—1,600 in a millimeter. Because the width of the grooves is similar to wavelengths of visible light, they form a diffraction grating. That is why you see rainbows on a CD. The colors are attractive, but they are incidental to the functions of storing and retrieving audio and other data.
The grooves are actually one continuous groove that spirals outward from the center. Data are recorded in the grooves as binary code (zeroes and ones) in small pits. Information in the pits is detected by a laser that tracks along the groove. It gets even more complicated: The speed of rotation must be varied as the laser tracks toward the circumference so that the linear speed along the groove remains constant. There is also an error correction mechanism to prevent the laser beam from getting off track. A diffraction grating is used to create the first two maxima on either side of the track. If those maxima are not the same distance from the track, an error is indicated and then corrected.
The pits are reflective because they have been coated with a thin layer of aluminum. That allows the laser beam to be reflected back and directed toward a photodiode detector. The signal can then be processed and converted to the audio we hear.
The longest wavelength of visible light is about 780 nm . How does that compare to the distance between CD grooves?
- The grooves are about 3 times the longest wavelength of visible light.
- The grooves are about 2 times the longest wavelength of visible light.
- The grooves are about 2 times the shortest wavelength of visible light.
- The grooves are about 3 times the shortest wavelength of visible light.
Links To Physics
Biology: DIC Microscopy
If you were completely transparent, it would be hard to recognize you from your photograph. The same problem arises when using a traditional microscope to view or photograph small transparent objects such as cells and microbes. Microscopes using differential interference contrast (DIC) solve the problem by making it possible to view microscopic objects with enhanced contrast, as shown in Figure 17.19.
A DIC microscope separates a polarized light source into two beams polarized at right angles to each other and coherent with each other, that is, in phase. After passing through the sample, the beams are recombined and realigned so they have the same plane of polarization. They then create an interference pattern caused by the differences in their optical path and the refractive indices of the parts of the sample they passed through. The result is an image with contrast and shadowing that could not be observed with traditional optics.
Where are diffraction gratings used? Diffraction gratings are key components of monochromators—devices that separate the various wavelengths of incoming light and allow a beam with only a specific wavelength to pass through. Monochromators are used, for example, in optical imaging of particular wavelengths from biological or medical samples. A diffraction grating can be chosen to specifically analyze a wavelength of light emitted by molecules in diseased cells in a biopsy sample, or to help excite strategic molecules in the sample with a selected frequency of light. Another important use is in optical fiber technologies where fibers are designed to provide optimum performance at specific wavelengths. A range of diffraction gratings is available for selecting specific wavelengths for such use.
Diffraction gratings are used in spectroscopes to separate a light source into its component wavelengths. When a material is heated to incandescence, it gives off wavelengths of light characteristic of the chemical makeup of the material. A pure substance will produce a spectrum that is unique, thus allowing identification of the substance. Spectroscopes are also used to measure wavelengths both shorter and longer than visible light. Such instruments have become especially useful to astronomers and chemists. Figure 17.20 shows a diagram of a spectroscope.
Light diffracts as it moves through space, bending around obstacles and interfering constructively and destructively. While diffraction allows light to be used as a spectroscopic tool, it also limits the detail we can obtain in images.
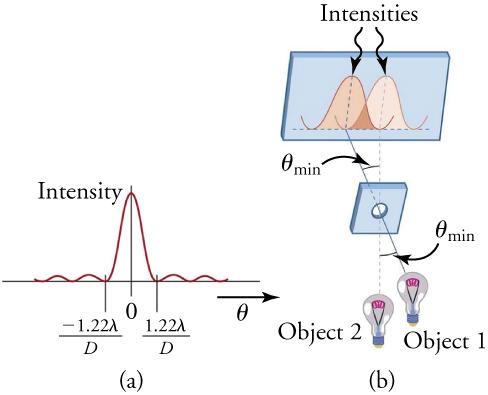
Figure 17.21 (a) shows the effect of passing light through a small circular aperture. Instead of a bright spot with sharp edges, a spot with a fuzzy edge surrounded by circles of light is obtained. This pattern is caused by diffraction similar to that produced by a single slit. Light from different parts of the circular aperture interferes constructively and destructively. The effect is most noticeable when the aperture is small, but the effect is there for large apertures, too.
How does diffraction affect the detail that can be observed when light passes through an aperture? Figure 17.21 (b) shows the diffraction pattern produced by two point light sources that are close to one another. The pattern is similar to that for a single point source, and it is just barely possible to tell that there are two light sources rather than one. If they are closer together, as in Figure 17.21 (c), you cannot distinguish them, thus limiting the detail, or resolution, you can obtain. That limit is an inescapable consequence of the wave nature of light.
There are many situations in which diffraction limits the resolution. The acuity of vision is limited because light passes through the pupil, the circular aperture of the eye. Be aware that the diffraction-like spreading of light is due to the limited diameter of a light beam, not the interaction with an aperture. Thus light passing through a lens with a diameter of D shows the diffraction effect and spreads, blurring the image, just as light passing through an aperture of diameter D does. Diffraction limits the resolution of any system having a lens or mirror. Telescopes are also limited by diffraction, because of the finite diameter, D, of their primary mirror.
- The bands produced by diffraction gratings are dimmer but sharper than the bands produced by two slits.
- The bands produced by diffraction gratings are brighter, though less sharp, than the bands produced by two slits.
- The bands produced by diffraction gratings are brighter and sharper than the bands produced by two slits.
- The bands produced by diffraction gratings are dimmer and less sharp, but more widely dispersed, than the bands produced by two slits.
Calculations Involving Diffraction Gratings and Resolution
Calculations Involving Diffraction Gratings and Resolution
Early in the chapter, it was mentioned that when light passes from one medium to another, its speed and wavelength change, but its frequency remains constant. The equation
shows how to the wavelength in a given medium, , is related to the wavelength in a vacuum, , and the refractive index, n, of the medium. The equation is useful for calculating the change in wavelength of a monochromatic laser beam in various media. The analysis of a diffraction grating is very similar to that for a double slit. As you know from the discussion of double slits in Young’s double-slit experiment, light is diffracted by, and spreads out after passing through, each slit. Rays travel at an angle relative to the incident direction. Each ray travels a different distance to a common point on a screen far away. The rays start in phase, and they can be in or out of phase when they reach a screen, depending on the difference in the path lengths traveled. Each ray travels a distance that differs by from that of its neighbor, where d is the distance between slits. If equals an integral number of wavelengths, the rays all arrive in phase, and constructive interference (a maximum) is obtained. Thus, the condition necessary to obtain constructive interference for a diffraction grating is
where d is the distance between slits in the grating, is the wavelength of the light, and m is the order of the maximum. Note that this is exactly the same equation as for two slits separated by d. However, the slits are usually closer in diffraction gratings than in double slits, producing fewer maxima at larger angles.
Watch Physics
Diffraction Grating
This video explains the geometry behind the diffraction pattern produced by a diffraction grating.
- It is the same as the equation for destructive interference for a double-slit diffraction pattern.
- It is the same as the equation for constructive interference for a double-slit diffraction pattern.
- It is the same as the equation for constructive interference for a single-slit diffraction pattern.
- It is the same as the equation for destructive interference for a single-slit diffraction pattern.
Just what is the resolution limit of an aperture or lens? To answer that question, consider the diffraction pattern for a circular aperture, which, similar to the diffraction pattern of light passing through a slit, has a central maximum that is wider and brighter than the maxima surrounding it (see Figure 17.21 (a)). It can be shown that, for a circular aperture of diameter D, the first minimum in the diffraction pattern occurs at , provided that the aperture is large compared with the wavelength of light, which is the case for most optical instruments. The accepted criterion for determining the diffraction limit to resolution based on diffraction was developed by Lord Rayleigh in the 19th century. The Rayleigh criterion for the diffraction limit to resolution states that two images are just resolvable when the center of the diffraction pattern of one is directly over the first minimum of the diffraction pattern of the other. See Figure 17.22 (b). The first minimum is at an angle of , so that two point objects are just resolvable if they are separated by the angle
where is the wavelength of the light (or other electromagnetic radiation) and D is the diameter of the aperture, lens, mirror, etc., with which the two objects are observed. In the expression above, has units of radians.
Snap Lab
Resolution
- A sheet of white paper
- A black pen or pencil
- A measuring tape
Instructions
- Draw two lines several mm apart on a white sheet of paper.
- Move away from the sheet as it is held upright, and measure the distance at which you can just distinguish (resolve) the lines as separate.
- Use to calculate D the diameter of your pupil. Use the distance between the lines and the maximum distance at which they were resolved to calculate . Use the average wavelength for visible light as the value for .
- Compare your answer to the average pupil diameter of 3 mm.
- The limit for resolution is when the minimum of the pattern for one of the lines is directly over the first minimum of the pattern for the other line.
- The limit for resolution is when the maximum of the pattern for one of the lines is directly over the first minimum of the pattern for the other line.
- The limit for resolution is when the maximum of the pattern for one of the lines is directly over the second minimum of the pattern for the other line.
- The limit for resolution is when the minimum of the pattern for one of the lines is directly over the second maximum of the pattern for the other line.
Worked Example
Change of Wavelength
A monochromatic laser beam of green light with a wavelength of 550 nm passes from air to water. The refractive index of water is 1.33. What will be the wavelength of the light after it enters the water?
STRATEGY
You can assume that the refractive index of air is the same as that of light in a vacuum because they are so close. You then have all the information you need to solve for .
The refractive index of air is 1.0003, so the approximation holds for three significant figures. You would not see the light change color, however. Color is determined by frequency, not wavelength.
Worked Example
Diffraction Grating
A diffraction grating has 2000 lines per centimeter. At what angle will the first-order maximum form for green light with a wavelength of 520 nm?
STRATEGY
You are given enough information to calculate d, and you are given the values of and m. You will have to find the arcsin of a number to find .
First find d.
Rearrange the equation for constructive interference conditions for a diffraction grating, and substitute the known values.
This angle seems reasonable for the first maximum. Recall that the meaning of sin‒1 (or arcsin) is the angle with a sine that is (the unknown). Remember that the value of will not be greater than 1 for any value of .
Worked Example
Resolution
What is the minimum angular spread of a 633-nm-wavelength He-Ne laser beam that is originally 1.00 mm in diameter?
STRATEGY
The diameter of the beam is the same as if it were coming through an aperture of that size, so D = 1.00 mm. You are given , and you must solve for .
The conversion factor for radians to degrees is 1.000 radian = 57.3°. The spread is very small and would not be noticeable over short distances. The angle represents the angular separation of the central maximum and the first minimum.
Practice Problems
Practice Problems
A beam of yellow light has a wavelength of 600 nm in a vacuum and a wavelength of 397 nm in Plexiglas. What is the refractive index of Plexiglas?
- 1.51
- 2.61
- 3.02
- 3.77
What is the angle between two just-resolved points of light for a 3.00 mm diameter pupil, assuming an average wavelength of 550 nm?
- 224 rad
- 183 rad
- 1.83 × 10–4 rad
- 2.24 × 10–4 rad
Check Your Understanding
Check Your Understanding
- The pattern is colorful.
- The pattern is faded.
- The pattern is sharper.
- The pattern is curved.
- Light is always polarized.
- Light is always reflected.
- Light is always refracted.
- Light is always diffracted.
- The pattern formed has broader and brighter bands.
- The pattern formed has broader and duller bands.
- The pattern formed has narrower and duller bands.
- The pattern formed has narrower and brighter bands.
- The slits in a diffraction grating are broader, with space between them that is greater than the separation of the two slits in two-slit diffraction.
- The slits in a diffraction grating are broader, with space between them that is the same as the separation of the two slits in two-slit diffraction.
- The slits in a diffraction grating are narrower, with space between them that is the same as the separation of the two slits in two-slit diffraction.
- The slits in a diffraction grating are narrower, with space between them that is greater than the separation of the two slits in two-slit diffraction.